
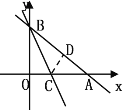
【题目】如图,一次函数的图像与x轴、y轴分别交于A、B两点,且A、B的坐标分别为(4,0),(0,3).
(1)求一次函数的表达式.
(2)点C在线段OA上,沿BC将△OBC翻折,O点恰好落在AB上的D处,
求直线BC的表达式.
【答案】(1)y=![]() x+3; (2)BC直线解析式y=-2x+3.
x+3; (2)BC直线解析式y=-2x+3.
【解析】
试题(1)把A,B两点坐标代入一次函数解析式可得相关值;(2)作DE⊥OA于E,利用图形可得DE,AE的值,利用勾股定理可得OC的值,也就求得了C的坐标,代入解析式可得BC的解析式.
试题解析:(1)(1)设一次函数的解析式为y=kx+b,分别把A(4,0),B(0,3)代入得0=4k+b,解得3=b,
∴b=3,k="-"![]() , ∴y=-
, ∴y=-![]() x+3 2分
x+3 2分
(2)在Rt△AOB中,AB=5 3分
∵翻折
∴BD=OB=3,OC=DC,∠BDC=∠B0C=90°
∴AD=5-3=2,
设OC=X,在Rt△CDA中![]()
∴![]()
∴![]()
∴C![]() 6分
6分
∴BC直线解析式![]() 8分
8分


科目:初中数学 来源: 题型:
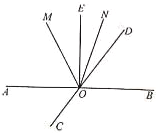
【题目】如图,直线AB、CD相交于点O,∠BOE=90°,OM平分∠AOD,ON平分∠DOE.
(1)若∠MOE=27°,求∠AOC的度数;
(2)当∠BOD=x°(0<x<90)时,求∠MON的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是正方形ABCD的对角线BD上的一个动点(不与B、D重合),连结AP,过点B作直线AP的垂线,垂足为H,连结DH.若正方形的边长为4,则线段DH长度的最小值是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级为了开展球类兴趣小组,需要购买一批足球和篮球﹒若购买3个足球和5个篮球需580元;若购买4个足球和3个篮球需480元.
(1)求出足球和篮球的的单价分别是多少?
(2)已知该年级决定用800元购进这两种球,若两种球都要有,请问有几种购买方案,并请加以说明﹒
查看答案和解析>>
科目:初中数学 来源: 题型:
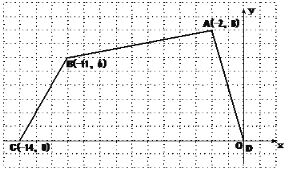
【题目】四边形ABCD各个顶点的坐标分别为A(-2,8),B(-11,6),C(-14,0),D(0,0)。
(1)确定这个四边形的面积,你是怎么做的?
(2)如果把原来ABCD各个顶点纵坐标保持不变,横坐标增加2,所得的四边形面积又是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按下面的程序计算:当输入x=100 时,输出结果是299;当输入x=50时,输出结果是446;如果输入 x 的值是正整数,输出结果是257,那么满足条件的x的值最多有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣2x+7与x轴、y轴分别相交于点C、B,与直线y=![]() x相交于点A.
x相交于点A.
(1)求A点坐标;
(2)求△OAC的面积;
(3)如果在y轴上存在一点P,使△OAP是以OA为底边的等腰三角形,求P点坐标;
(4)在直线y=﹣2x+7上是否存在点Q,使△OAQ的面积等于6?若存在,请求出Q点的坐标,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=30°,以直角边AB为直径作半圆交AC于点D,以AD为边作等边△ADE,延长ED交BC于点F,BC=2 ![]() ,则图中阴影部分的面积为 . (结果不取近似值)
,则图中阴影部分的面积为 . (结果不取近似值) 
查看答案和解析>>
科目:初中数学 来源: 题型:
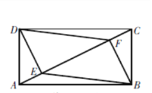
【题目】如图,一块长方形场地ABCD的长AB与宽AD的比为2∶1,DE⊥AC于点E,BF⊥AC于点F,连结BE,DF,则四边形DEBF与长方形ABCD的面积比为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com