
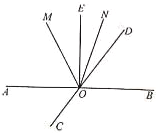
【题目】如图,直线AB、CD相交于点O,∠BOE=90°,OM平分∠AOD,ON平分∠DOE.
(1)若∠MOE=27°,求∠AOC的度数;
(2)当∠BOD=x°(0<x<90)时,求∠MON的度数.
【答案】(1)54°;(2)45°.
【解析】
(1)已知∠BOE=90°,根据平角的定义可得∠AOE =90°,又因∠MOE=27°,可求得∠AOM=63°;由OM平分∠AOD,根据角平分线的定义可得∠AOD=2∠AOM=126°,再由平角的定义即可求得∠AOC=54°;(2)已知∠BOD=x°,即可求得∠AOD=180°-x°,∠DOE=90°-x°;再由M平分∠AOD,ON平分∠DOE,根据角平分线的定义可得∠MOD =![]() (180°-x°),∠DON=
(180°-x°),∠DON=![]() (90°-x°),由∠MON=∠MOD+∠DON即可求得∠MON的度数.
(90°-x°),由∠MON=∠MOD+∠DON即可求得∠MON的度数.
(1)∵∠BOE=90°,
∴∠AOE=180°-∠BOE=90°,
∵∠MOE=27°,
∴∠AOM=90°-∠MOE=90°-27°=63°,
∵OM平分∠AOD,
∴∠AOD=2∠AOM=126°,
∴∠AOC=180°-∠AOD=180°-126°=54°;
(2)∵∠BOD=x°,
∴∠AOD=180°-x°,
∵OM平分∠AOD,
∴∠MOD=![]() ∠AOD=
∠AOD=![]() (180°-x°),
(180°-x°),
∵∠BOE=90°,∠BOD=x°
∴∠DOE=90°-x°;
∵ON平分∠DOE,
∴∠DON=![]() (90°-x°).
(90°-x°).
∴∠MON=∠MOD+∠DON=![]() (180°-x°)-
(180°-x°)-![]() (90°-x°)=45°.
(90°-x°)=45°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,阶梯图的每个台阶上都标着一个数,从下到上的第1个至第4个台阶上依次标着﹣5,﹣2,1,9,且任意相邻四个台阶上数的和都相等.
尝试 (1)求前4个台阶上数的和是多少?
(2)求第5个台阶上的数x是多少?
应用 求从下到上前31个台阶上数的和.
发现 试用含k(k为正整数)的式子表示出数“1”所在的台阶数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有甲、乙两个瓷器店出售茶壶和茶杯,茶壶每只价格为20元,茶杯每只价格为5元,已知甲店制定的优惠方法是买一只茶壶送一只茶杯,乙店按总价的92%付款.学校办公室需要购买茶壶4只,茶杯若干只(不少于4只).
(1)当购买多少只茶杯时,两店的优惠方法付款一样多?
(2)当需要购买40只茶杯时,若让你去办这件事,你打算去哪家商店购买?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,已知AD是角平分线,∠B=66°,∠C=54°.
(1)求∠ADB的度数;
(2)若DE⊥AC于点E,求∠ADE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育课上全班男生进行了百米测试,达标成绩为14秒,下面是第一小组8名男生的成绩记录,其中“+”表示成绩大于14秒,“-”表示成绩小于14秒.
![]()
(1)求这个小组男生百米测试的达标率是多少?
(2)求这个小组8名男生的平均成绩是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
= y2+8y+16 (第二步)
=(y+4)2 (第三步)
=(x2-4x+4)2 (第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
A.提取公因式
B.平方差公式
C.两数和的完全平方公式
D.两数差的完全平方公式
(2)该同学因式分解的结果是否彻底?________.(填“彻底”或“不彻底”)
若不彻底,请直接写出因式分解的最后结果_________.
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
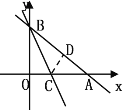
【题目】如图,一次函数的图像与x轴、y轴分别交于A、B两点,且A、B的坐标分别为(4,0),(0,3).
(1)求一次函数的表达式.
(2)点C在线段OA上,沿BC将△OBC翻折,O点恰好落在AB上的D处,
求直线BC的表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com