
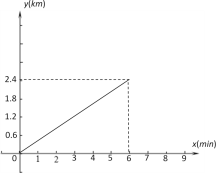
【题目】已知A、B两地相距2.4km,甲骑车匀速从A地前往B地,如图表示甲骑车过程中离A地的路程y(km)与他行驶所用的时间x(min)之间的关系.根据图像解答下列问题:
(1)甲骑车的速度是 km/min;
(2)若在甲出发时,乙在甲前方0.6km处,两人均沿同一路线同时出发匀速前往B地,在第3分钟甲追上了乙,两人到达B地后停止.请在下面同一平面直角坐标系中画出乙离A地的距离y乙(km)与所用时间x(min)的关系的大致图像;
(3)乙在第几分钟到达B地?
(4)两人在整个行驶过程中,何时相距0.2km?
【答案】(1)0.4(2)见解析(3)9分钟 (4)2分钟,4分钟,8分钟.
【解析】
(1)根据速度等于路程除以时间进行解答即可;
(2)根据“在甲出发时,乙在甲前方0.6km处”可知过点(0,0.6),根据“在第3分钟甲追上了乙”可知该图像过横坐标为3的点,过着两点即可画出;
(3)求出y甲=0.4x,把x=3代入y=0.4x,求得y=1.2,再求出 y乙=0.2x+0.6,把y=2.4代入y乙=0.2x+0.6得x=9,所以乙在第9分钟到达B地;
(4)分三种情况,相遇前,相遇后和甲到达后相距0.2km.
解:(1)0.4,
(2)如图:
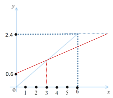
(3)设甲的函数的表达式为y甲=kx,然后把x=6,y=2.4代入求得k=0.4,所以函数表达式为y甲=0.4x,把x=3代入y=0.4x,求得y=1.2,
设乙的函数表达式为y乙=kx+b,然后把x=0,y=0.6;x=3,y=1.2分别代入
求得k=0.2,b=0.6,所以函数表达式为y乙=0.2x+0.6,
把y=2.4代入y乙=0.2x+0.6得x=9,
所以乙在第9分钟到达B地.
(4)①相遇前是y乙-y甲=0.2即0.2x+0.6-0.4x=0.2,解得x=2,
所以在第2分钟两人相距0.2km;
②相遇后是y甲-y乙=0.2即0.4x-(0.2x+0.6)=0.2,解得x=4,
所以在第4分钟两人相距0.2km.
③把y=2.2代入y乙=0.2x+0.6得x=8,
所以第8分钟时两人相距0.2km.


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】在等腰△ABC中,AC=BC,以BC为直径的⊙O分别与AB,AC相交于点D,E,过点D作DF⊥AC,垂足为点F. 
(1)求证:DF是⊙O的切线;
(2)分别延长CB,FD,相交于点G,∠A=60°,⊙O的半径为6,求阴影部分的面积. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级为了开展球类兴趣小组,需要购买一批足球和篮球﹒若购买3个足球和5个篮球需580元;若购买4个足球和3个篮球需480元.
(1)求出足球和篮球的的单价分别是多少?
(2)已知该年级决定用800元购进这两种球,若两种球都要有,请问有几种购买方案,并请加以说明﹒
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按下面的程序计算:当输入x=100 时,输出结果是299;当输入x=50时,输出结果是446;如果输入 x 的值是正整数,输出结果是257,那么满足条件的x的值最多有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣2x+7与x轴、y轴分别相交于点C、B,与直线y=![]() x相交于点A.
x相交于点A.
(1)求A点坐标;
(2)求△OAC的面积;
(3)如果在y轴上存在一点P,使△OAP是以OA为底边的等腰三角形,求P点坐标;
(4)在直线y=﹣2x+7上是否存在点Q,使△OAQ的面积等于6?若存在,请求出Q点的坐标,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①是一块瓷砖的图案,用这种瓷砖来铺设地面,如果铺成一个2×2的正方形图案(如图②),其中完整的圆共有5个,如果铺成一个3×3的正方形图案(如图③),其中完整的圆共有13个,如果铺成一个4×4的正方形图案(如图④),其中完整的圆共有25个,若这样铺成一个10×10的正方形图案,则其中完整的圆共有( )个.
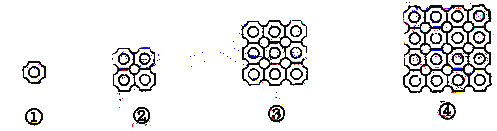
A.145 B.146 C.180 D.181
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=30°,以直角边AB为直径作半圆交AC于点D,以AD为边作等边△ADE,延长ED交BC于点F,BC=2 ![]() ,则图中阴影部分的面积为 . (结果不取近似值)
,则图中阴影部分的面积为 . (结果不取近似值) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知 ![]() 内接于
内接于 ![]() ,
, ![]() 是直径,点
是直径,点 ![]() 在
在 ![]() 上,
上, ![]() ,过点
,过点 ![]() 作
作 ![]() ,垂足为
,垂足为 ![]() ,连接
,连接 ![]() 交
交 ![]() 边于点
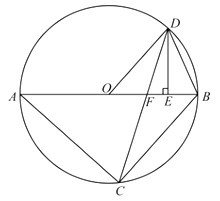
边于点 ![]() .
.
(1)求证: ![]() ∽
∽ ![]() ;
;
(2)求证: ![]() ;
;
(3)连接 ![]() ,设
,设 ![]() 的面积为
的面积为 ![]() ,四边形
,四边形 ![]() 的面积为
的面积为 ![]() ,若
,若 ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com