
【题目】如图,在△ABC中,点D,点E分别是AB,AC的中点,点F是DE上一点,∠AFC=90°,BC=10cm,AC=6cm,则DF=cm.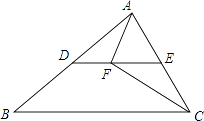
【答案】2
【解析】解:方法一:如图,延长AF交BC于H, 
∵点D,点E分别是AB,AC的中点,
∴DE是△ABC的中位线,
∴AF=FH,
∵∠AFC=90°,
∴CF垂直平分AH,
∴CH=AC=6cm,
∵BC=10cm,
∴BH=BC﹣CH=10﹣6=4cm,
在△ABH中,DF是中位线,
∴DF= ![]() BH=
BH= ![]() ×4=2cm;
×4=2cm;
方法二:∵点D,点E分别是AB,AC的中点,
∴DE是△ABC的中位线,
∴DE= ![]() BC=
BC= ![]() ×10=5cm,
×10=5cm,
∵∠AFC=90°,E是AC的中点,
∴EF= ![]() AC=
AC= ![]() ×6=3cm,
×6=3cm,
∴DF=DE﹣EF=5﹣3=2cm.
所以答案是:2.
【考点精析】掌握直角三角形斜边上的中线和三角形中位线定理是解答本题的根本,需要知道直角三角形斜边上的中线等于斜边的一半;连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.


科目:初中数学 来源: 题型:
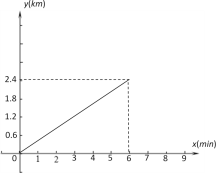
【题目】已知A、B两地相距2.4km,甲骑车匀速从A地前往B地,如图表示甲骑车过程中离A地的路程y(km)与他行驶所用的时间x(min)之间的关系.根据图像解答下列问题:
(1)甲骑车的速度是 km/min;
(2)若在甲出发时,乙在甲前方0.6km处,两人均沿同一路线同时出发匀速前往B地,在第3分钟甲追上了乙,两人到达B地后停止.请在下面同一平面直角坐标系中画出乙离A地的距离y乙(km)与所用时间x(min)的关系的大致图像;
(3)乙在第几分钟到达B地?
(4)两人在整个行驶过程中,何时相距0.2km?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种产品的年产量不超过1 000t,该产品的年产量(t)与费用(万元)之间的函数关系如图(1);该产品的年销售量(t)与每吨销售价(万元)之间的函数关系如图(2).若生产出的产品都能在当年销售完,则年产量为多少吨时,当年可获得7500万元毛利润?(毛利润=销售额﹣费用)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一轮船由![]() 处向
处向![]() 处航行,在
处航行,在![]() 处测得
处测得![]() 处在
处在![]() 的北偏东
的北偏东![]() 方向上,在海岛上的观察所
方向上,在海岛上的观察所![]() 测得
测得![]() 在
在![]() 的南偏西
的南偏西![]() 方向上,
方向上,![]() 在
在![]() 的南偏东
的南偏东![]() 方向.若轮船行驶到
方向.若轮船行驶到![]() 处,那么从
处,那么从![]() 处看
处看![]() ,
,![]() 两处的视角
两处的视角![]() 是多少度?
是多少度?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠BOC=60°,OF平分∠BOC.若AO⊥BO,OE平分∠AOC,则∠EOF的度数是( )
A. 45°
B. 15°
C. 30°或60°
D. 45°或15°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,E、F分别是边AD、DC上的点,且AF⊥BE.
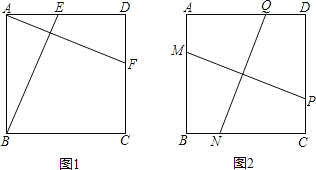
(1)求证:AF=BE;
(2)如图2,在正方形ABCD中,M、N、P、Q分别是边AB、BC、CD、DA上的点,且MP⊥NQ.MP与NQ是否相等?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC和△DBC中,∠ACB=∠DBC=90°,点E是BC的中点,EF⊥AB,垂足为F,且AB=DE.

(1)求证:△BCD是等腰直角三角形;
(2)若BD=8厘米,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的两条对角线AC和BD相交于点O,并且BD=4,AC=6,BC= ![]() .
.
(1)AC与BD有什么位置关系?为什么?
(2)四边形ABCD是菱形吗?为什么.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com