
【题目】如图,平行四边形ABCD的两条对角线AC和BD相交于点O,并且BD=4,AC=6,BC= ![]() .
.
(1)AC与BD有什么位置关系?为什么?
(2)四边形ABCD是菱形吗?为什么.
【答案】
(1)解:结论:AC⊥BD. 
理由:∵四边形ABCD是平行四边形,
∴BO=DO=2,AO=CO=3,
∵BC= ![]() ,
,
∴BO2+CO2=CB2,
∴∠BOC=90°,
∴BD⊥AC,
(2)解:是菱形.理由如下:
∵BD⊥AC,四边形ABCD是平行四边形,
∴四边形ABCD是菱形.
【解析】(1)题中已知平行四边形的两对角线的长,根据平行四边形的对角线互相平分,求出OB、OC的长,再利用勾股定理的逆定理证明△BOC是直角三角形,即可得出结论。
(2)由(1)的结论BD⊥AC及已知四边形ABCD是平行四边形,可证明四边形ABCD是菱形。
【考点精析】关于本题考查的勾股定理的逆定理和平行四边形的性质,需要了解如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形;平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分才能得出正确答案.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
【题目】下列各式中:
①由3x=﹣4系数化为1得x=﹣![]() ;
;
②由5=2﹣x移项得x=5﹣2;
③由![]() 去分母得2(2x﹣1)=1+3(x﹣3);
去分母得2(2x﹣1)=1+3(x﹣3);
④由2(2x﹣1)﹣3(x﹣3)=1去括号得4x﹣2﹣3x﹣9=1.
其中正确的个数有( )
A. 0个 B. 1个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车行驶时油箱中余油量Q(升)与行驶时间t(小时)的关系如下表:
行驶时间t | 1 | 2 | 3 | 4 | … |
余油量Q | 40﹣6 | 40﹣12 | 40﹣18 | 40﹣24 | … |
(1)写出用行驶时间t表示余油量Q的代数式 ;
(2)当t=![]() 时,余油量Q的值为 升;
时,余油量Q的值为 升;
(3)汽车每小时行驶60公里,问油箱中原有汽油可供汽车行驶多少公里?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,⊙P的圆心是(2,a)(a>2),半径为2,函数y=x的图象被⊙P截得的弦AB的长为 ![]() ,则a的值是( )
,则a的值是( )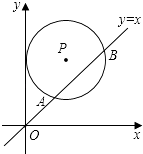
A.2 ![]()
B.2+ ![]()
C.2 ![]()
D.2+ ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,BC>AB>AC.甲、乙两人想在BC上取一点P,使得∠APC=2∠ABC,其作法如下: (甲)作AB的中垂线,交BC于P点,则P即为所求
(乙)以B为圆心,AB长为半径画弧,交BC于P点,则P即为所求
对于两人的作法,下列判断何者正确?( )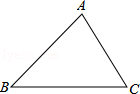
A.两人皆正确
B.两人皆错误
C.甲正确,乙错误
D.甲错误,乙正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果批发商场经销一种高档水果,如果每千克盈利10元,每天可售出500千克.经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克.
(1)现该商场要保证每天盈利6 000元,同时又要顾客得到实惠,那么每千克应涨价多少元?
(2)若该商场单纯从经济角度看,每千克这种水果涨价多少元,能使商场获利最多?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com