
【题目】如图,在平面直角坐标系中,⊙P的圆心是(2,a)(a>2),半径为2,函数y=x的图象被⊙P截得的弦AB的长为 ![]() ,则a的值是( )
,则a的值是( )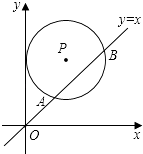
A.2 ![]()
B.2+ ![]()
C.2 ![]()
D.2+ ![]()
【答案】B
【解析】解:过P点作PE⊥AB于E,过P点作PC⊥x轴于C,交AB于D,连接PA.
∵PE⊥AB,AB=2 ![]() ,半径为2,
,半径为2,
∴AE= ![]() AB=
AB= ![]() ,PA=2,
,PA=2,
根据勾股定理得:PE= ![]() =1,
=1,
∵点A在直线y=x上,
∴∠AOC=45°,
∵∠DCO=90°,
∴∠ODC=45°,
∴△OCD是等腰直角三角形,
∴OC=CD=2,
∴∠PDE=∠ODC=45°,
∴∠DPE=∠PDE=45°,
∴DE=PE=1,
∴PD= ![]() .
.
∵⊙P的圆心是(2,a),
∴a=PD+DC=2+ ![]() .
.
故选:B.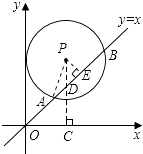
【考点精析】根据题目的已知条件,利用圆的定义和直线与圆的三种位置关系的相关知识可以得到问题的答案,需要掌握平面上到定点的距离等于定长的所有点组成的图形叫做圆.定点称为圆心,定长称为半径;直线与圆有三种位置关系:无公共点为相离;有两个公共点为相交,这条直线叫做圆的割线;圆与直线有唯一公共点为相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】解下列方程:
(1)2(10﹣0.5y)=﹣(1.5y+2)
(2)![]() (x﹣5)=3﹣
(x﹣5)=3﹣![]() (x﹣5)
(x﹣5)
(3)![]() ﹣1=
﹣1=![]()
(4)x﹣![]() (x﹣9)=
(x﹣9)=![]() [x+
[x+![]() (x﹣9)]
(x﹣9)]
(5) ![]() -
-![]() =0.5x+2
=0.5x+2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为创建“国家园林城市”,某校举行了以“爱我黄石”为主题的图片制作比赛,评委会对200名同学的参赛作品打分发现,参赛者的成绩x均满足50≤x<100,并制作了频数分布直方图,如图.
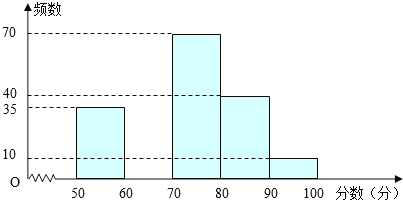
根据以上信息,解答下列问题:
(1)请补全频数分布直方图;
(2)若依据成绩,采取分层抽样的方法,从参赛同学中抽40人参加图片制作比赛总结大会,则从成绩80≤x<90的选手中应抽多少人?
(3)比赛共设一、二、三等奖,若只有25%的参赛同学能拿到一等奖,则一等奖的分数线是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的两条对角线AC和BD相交于点O,并且BD=4,AC=6,BC= ![]() .
.
(1)AC与BD有什么位置关系?为什么?
(2)四边形ABCD是菱形吗?为什么.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知BD垂直平分线段AC,∠BCD=∠ADF,AF⊥AC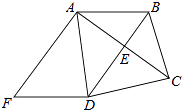
(1)证明:四边形ABDF是平行四边形;
(2)若AF=DF=5,AD=6,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.
(1)求证AD=AE;
(2)连接OA,BC,试判断直线OA,BC的关系并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AD∥BC,AB∥CD,E在线段BC延长线上,AE平分∠BAD.连接DE,若∠ADE=3∠CDE,∠AED=60°.
(1)求证:∠ABC=∠ADC;
(2)求∠CDE的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com