
【题目】如图,已知BD垂直平分线段AC,∠BCD=∠ADF,AF⊥AC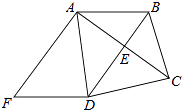
(1)证明:四边形ABDF是平行四边形;
(2)若AF=DF=5,AD=6,求AC的长.
【答案】
(1)证明:∵BD垂直平分AC, 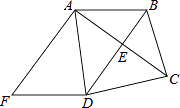
∴AB=BC,AD=DC,
在△ADB与△CDB中,
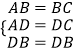 ,
,
∴△ADB≌△CDB(SSS)
∴∠BCD=∠BAD,
∵∠BCD=∠ADF,
∴∠BAD=∠ADF,
∴AB∥FD,
∵BD⊥AC,AF⊥AC,
∴AF∥BD,
∴四边形ABDF是平行四边形,
(2)解:∵四边形ABDF是平行四边形,AF=DF=5,
∴ABDF是菱形,
∴AB=BD=5,
∵AD=6,
设BE=x,则DE=5﹣x,
∴AB2﹣BE2=AD2﹣DE2,
即52﹣x2=62﹣(5﹣x)2
解得:x= ![]() ,
,
∴AE= ![]() =
= ![]() ,
,
∴AC=2AE= ![]() .
.
【解析】(1)根据线段垂直平分线上的点到相线段两端点的距离相等,得出AB=BC,AD=DC,即可证得△ADB≌△CDB,得出对应角相等,再根据已知证明AB∥FD,AF∥BD,即可证得结论。
(2)根据一组邻边相等的平行四边形是菱形,可知ABDF是菱形,BD=DF=5,然后在Rt△ABE和Rt△ADE中,利用勾股定理,得出AE2=AB2﹣BE2=AD2﹣DE2,设BE=x,建立方程,求出BE的长,再求出AE的长,根据AC=2AE,即可求得结果。
【考点精析】通过灵活运用线段垂直平分线的性质和勾股定理的概念,掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2即可以解答此题.


科目:初中数学 来源: 题型:
【题目】如图所示,在⊙O中, ![]() =
= ![]() ,弦AB与弦AC交于点A,弦CD与AB交于点F,连接BC.
,弦AB与弦AC交于点A,弦CD与AB交于点F,连接BC. 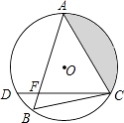
(1)求证:AC2=ABAF;
(2)若⊙O的半径长为2cm,∠B=60°,求图中阴影部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把宽为2cm 的刻度尺在圆O上移动,当刻度尺的一边EF与圆O相切于A时,另一边与圆的两个交点处的度刻恰好为“2”(C点)和“8”(B点)(单位:cm ),则该圆的半径是( ) 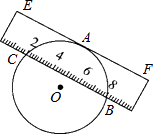
A.3 cm
B.3.25 cm
C.2 ![]() cm
cm
D.4 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,⊙P的圆心是(2,a)(a>2),半径为2,函数y=x的图象被⊙P截得的弦AB的长为 ![]() ,则a的值是( )
,则a的值是( )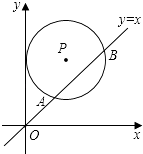
A.2 ![]()
B.2+ ![]()
C.2 ![]()
D.2+ ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,点B为劣弧AN的中点.P是直径MN上一动点,则PA+PB的最小值为( )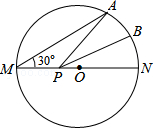
A.![]()
B.1
C.2
D.2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在直角三角形ABC中,∠ACB=90°,D是AB上一点,且∠ACD=∠B.
(1)如图1,求证:CD⊥AB;
(2)将△ADC沿CD所在直线翻折,A点落在BD边所在直线上,记为A′点.
①如图2,若∠B=34°,求∠A′CB的度数;
②若∠B=n°,请直接写出∠A′CB的度数(用含n的代数式表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
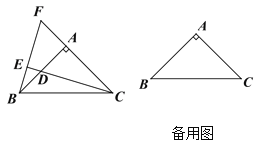
【题目】如图,△ABC中,AB=AC,∠BAC=90°,点D是直线AB上的一动点(不和A、B重合),BE⊥CD于E,交直线AC于F
(1)点D在边AB上时,试探究线段BD、AB和AF的数量关系,并证明你的结论;
(2)点D在AB的延长线或反向延长线上时,(1)中的结论是否成立?若不成立,请写出正确结论并证明。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的坐标系中,△ABC的三个顶点的坐标依次为A(﹣1,2),B(﹣4,1),C(﹣2,﹣2).
(1)请在这个坐标系中作出△ABC关于y轴对称的△A1B1C1.
(2)分别写出点A1、B1、C1的坐标.
(3)求△A1B1C1的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com