练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】把宽为2cm 的刻度尺在圆O上移动，当刻度尺的一边EF与圆O相切于A时，另一边与圆的两个交点处的度刻恰好为“2”（C点）和“8”（B点）（单位：cm ），则该圆的半径是（ ）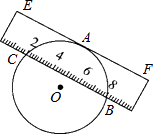
    A.3 cm
    B.3.25 cm
    C.2 cm
    D.4 cm

    【答案】B
    【解析】解：连接OA交BC于点E，

    设OB=r，

    ∵AB=8﹣2=6cm，OD⊥AB，

    ∴BE= AB= ×6=3cm，

    在Rt△BOE中，

    OE2+BE2=OB2，即（r﹣2）2+9=r2，

    解得r= =3.25cm．

    故选B．

    【考点精析】关于本题考查的勾股定理的概念和垂径定理，需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；垂径定理：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧才能得出正确答案．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】（7分）如图，EF//AD， ＝.求证：∠DGA+∠BAC=180°.请将说明过程填写完成.

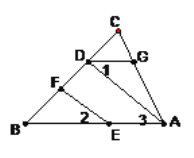
    证明：∵EF//AD，（已知）

    ∴＝_____(_____________________________).

    又∵＝（______）

    ∴＝（________________________）.

    ∴AB//______(____________________________)

    ∴∠DGA+∠BAC=180°(_____________________________)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

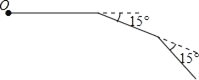
    【题目】如图，小明从点O出发，前进5m后向右转15°，再前进5m后又向右转15°，…这样一直下去，直到他第一次回到出发点O为止，他所走的路径构成了一个多边形．

    （1）小明一共走了多少米？

    （2）这个多边形的内角和是多少度？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知数轴上三点M，O，N对应的数分别为﹣2，0，4，点P为数轴上任意一点，其对应的数为x．

    （1）如果点P到点M点N的距离相等，则x＝　 　．

    （2）数轴上是否存在点P，使点P到点M、点N的距离之和是10？若存在，求出x的值；若不存在，请说明理由．

    （3）如果点P以每分钟1个单位长度的速度从点O向左运动，同时点M和点N分别以每分钟2个单位长度和每分钟3个单位长度的速度也向左运动．设t分钟时点P到点M、点N的距离相等，求t的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解下列方程：

    (1)2(10﹣0.5y)＝﹣(1.5y+2)

    (2)(x﹣5)＝3﹣(x﹣5)

    (3)﹣1＝

    (4)x﹣(x﹣9)＝[x+(x﹣9)]

    (5) -=0.5x+2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我市某化工厂从2015年开始节能减排，控制二氧化硫的排放．如图分别是该厂2015～2018年二氧化硫排放量(单位：吨)的两幅不完整的统计图，根据图中信息回答下列问题．

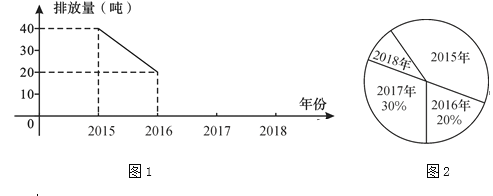
    (1)求该厂2015～2018年二氧化硫排放总量；

    (2)把图中折线统计图补充完整．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为创建“国家园林城市”，某校举行了以“爱我黄石”为主题的图片制作比赛，评委会对200名同学的参赛作品打分发现，参赛者的成绩x均满足50≤x＜100，并制作了频数分布直方图，如图．

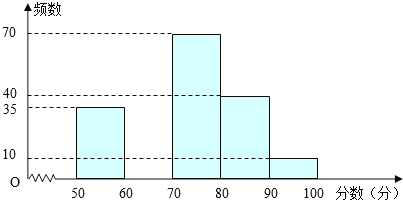
    根据以上信息，解答下列问题：

    （1）请补全频数分布直方图；

    （2）若依据成绩，采取分层抽样的方法，从参赛同学中抽40人参加图片制作比赛总结大会，则从成绩80≤x＜90的选手中应抽多少人？

    （3）比赛共设一、二、三等奖，若只有25%的参赛同学能拿到一等奖，则一等奖的分数线是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知BD垂直平分线段AC，∠BCD=∠ADF，AF⊥AC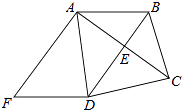

    （1）证明：四边形ABDF是平行四边形；
    （2）若AF=DF=5，AD=6，求AC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知，如图，A、B、C分别为数轴上的三点，A点对应的数为60，B点在A点的左侧，并且与A点的距离为30，C点在B点左侧，C点到A点距离是B点到A点距离的4倍．

    （1）求出数轴上B点对应的数及AC的距离．

    （2）点P从A点出发，以3单位/秒的速度向终点C运动，运动时间为t秒．

    ①当P点在AB之间运动时，则BP＝　 　．（用含t的代数式表示）

    ②P点自A点向C点运动过程中，何时P，A，B三点中其中一个点是另外两个点的中点？求出相应的时间t．

    ③当P点运动到B点时，另一点Q以5单位/秒的速度从A点出发，也向C点运动，点Q到达C点后立即原速返回到A点，那么Q点在往返过程中与P点相遇几次？直．接．写．出．相遇时P点在数轴上对应的数

    查看答案和解析>>

    同步练习册答案