
【题目】如图,AB是半圆O的直径,D是半圆上的一点,∠DOB=75°,DC交BA的延长线于E,交半圆于C,且CE=AO,求∠E的度数. 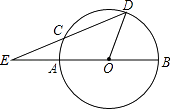
【答案】解:连结OC,如图,
∵CE=AO,
而OA=OC,
∴OC=EC,
∴∠E=∠1,
∴∠2=∠E+∠1=2∠E,
∵OC=OD,
∴∠D=∠2=2∠E,
∵∠BOD=∠E+∠D,
∴∠E+2∠E=75°,
∴∠E=25°.
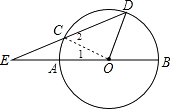
【解析】连结OC,如图,由CE=AO,OA=OC得到OC=EC,则根据等腰三角形的性质得∠E=∠1,再利用三角形外角性质得∠2=∠E+∠1=2∠E,加上∠D=∠2=2∠E,
所以∠BOD=∠E+∠D,即∠E+2∠E=75°,然后解方程即可.
【考点精析】解答此题的关键在于理解等腰三角形的性质的相关知识,掌握等腰三角形的两个底角相等(简称:等边对等角),以及对圆的定义的理解,了解平面上到定点的距离等于定长的所有点组成的图形叫做圆.定点称为圆心,定长称为半径.


科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC和△DBC中,∠ACB=∠DBC=90°,点E是BC的中点,EF⊥AB,垂足为F,且AB=DE.

(1)求证:△BCD是等腰直角三角形;
(2)若BD=8厘米,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的两条对角线AC和BD相交于点O,并且BD=4,AC=6,BC= ![]() .
.
(1)AC与BD有什么位置关系?为什么?
(2)四边形ABCD是菱形吗?为什么.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.
(1)求证AD=AE;
(2)连接OA,BC,试判断直线OA,BC的关系并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
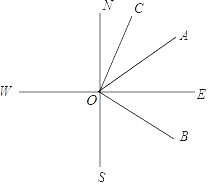
【题目】如图,直线SN⊥直线WE,垂足是点O,射线ON表示正北方向,射线OE表示正东方向.已知射线OB的方向是南偏东m°,射线OC的方向是北偏东n°,且m°的角与n°的角互余.
(1)写出图中与∠BOE互余的角: .
(2)若射线OA是∠BON的角平分线,探索∠BOS与∠AOC的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解填空,并在括号内填注理由.
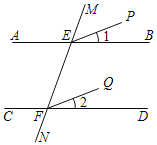
如图,已知AB∥CD,M,N分别交AB,CD于点E,F,∠1=∠2,求证:EP∥FQ.
证明:∵AB∥CD( )
∴∠MEB=∠MFD( ).
又∵∠1=∠2( )
∠MEB﹣∠1=∠MFD﹣∠2( )
即:∠MEP=∠
EP∥ .( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com