
【题目】如图1,在正方形ABCD中,E、F分别是边AD、DC上的点,且AF⊥BE.
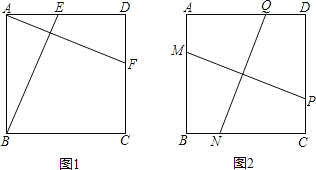
(1)求证:AF=BE;
(2)如图2,在正方形ABCD中,M、N、P、Q分别是边AB、BC、CD、DA上的点,且MP⊥NQ.MP与NQ是否相等?并说明理由.
【答案】解:(1)证明:在正方形ABCD中,AB=AD,∠BAE=∠D=90°,∴∠DAF+∠BAF=90°。
∵AF⊥BE,∴∠ABE+∠BAF=90°。∴∠ABE=∠DAF。
∵在△ABE和△DAF中,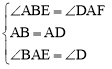 ,
,
∴△ABE≌△DAF(ASA)。
∴AF=BE。
(2)MP与NQ相等。理由如下:
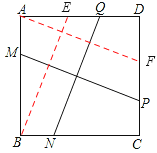
如图,过点A作AF∥MP交CD于F,过点B作BE∥NQ交AD于E,则四边形AMPF、BNQE都是是平行四边形,所以,MP=AF,NQ=BE,由(1)AF=BE,即得MP=NQ。
【解析】
试题(1)根据正方形的性质可得AB=AD,∠BAE=∠D=90°,再根据同角的余角相等求出∠ABE=∠DAF,然后利用“角边角”证明△ABE和△DAF全等,再根据全等三角形的证明即可。
(2)过点A作AF∥MP交CD于F,过点B作BE∥NQ交AD于E,则四边形AMPF、BNQE都是是平行四边形,所以,MP=AF,NQ=BE,由(1)AF=BE,即得MP=NQ。


 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=30°,以直角边AB为直径作半圆交AC于点D,以AD为边作等边△ADE,延长ED交BC于点F,BC=2 ![]() ,则图中阴影部分的面积为 . (结果不取近似值)
,则图中阴影部分的面积为 . (结果不取近似值) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一块长方形场地ABCD的长AB与宽AD的比为2∶1,DE⊥AC于点E,BF⊥AC于点F,连结BE,DF,则四边形DEBF与长方形ABCD的面积比为__________.
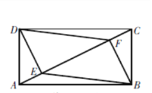
查看答案和解析>>
科目:初中数学 来源: 题型:
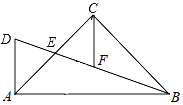
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的中点,AD⊥AB交BE延长线于点D,CF平分∠ACB交BD于点F,连接CD.
求证:(1)AD=CF;
(2)点F为BD的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
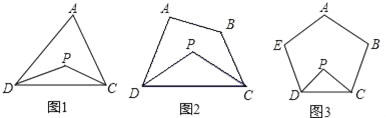
【题目】(1)已知:如图1,P为△ADC内一点,DP、CP分别平分∠ADC和∠ACD,如果∠A=90°,那么∠P=______°;如果∠A=x°,则∠P=____________°;(答案直接填在题中横线上)
(2)如图2,P为四边形ABCD内一点,DP、CP分别平分∠ADC和∠BCD,试探究∠P与∠A+∠B的数量关系,并写出你的探索过程;
(3)如图3,P为五边形ABCDE内一点,DP、CP分别平分∠EDC和∠BCD,请直接写出∠P与∠A+∠B+∠E的数量关系:________________;
(4)若P为n边形A1A2A3…An内一点,PA1平分∠AnA1A2,PA2平分∠A1A2A3,请直接写出∠P与∠A3+A4+A5+…∠An的数量关系:__________________________.(用含n的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式中:
①由3x=﹣4系数化为1得x=﹣![]() ;
;
②由5=2﹣x移项得x=5﹣2;
③由![]() 去分母得2(2x﹣1)=1+3(x﹣3);
去分母得2(2x﹣1)=1+3(x﹣3);
④由2(2x﹣1)﹣3(x﹣3)=1去括号得4x﹣2﹣3x﹣9=1.
其中正确的个数有( )
A. 0个 B. 1个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,BC>AB>AC.甲、乙两人想在BC上取一点P,使得∠APC=2∠ABC,其作法如下: (甲)作AB的中垂线,交BC于P点,则P即为所求
(乙)以B为圆心,AB长为半径画弧,交BC于P点,则P即为所求
对于两人的作法,下列判断何者正确?( )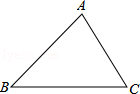
A.两人皆正确
B.两人皆错误
C.甲正确,乙错误
D.甲错误,乙正确
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com