
【题目】如图,BD是ABCD的对角线,AE⊥BD于E,CF⊥BD于F,求证:四边形AECF为平行四边形.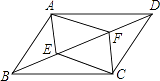
【答案】证明:
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABE=∠CDF,
∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°,AE∥CF,
在△AEB和△CFD中
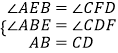
∴△AEB≌△CFD(AAS),
∴AE=CF,
∴四边形AECF是平行四边形.
【解析】要证四边形AECF为平行四边形.根据已知AE⊥BD,CF⊥BD,可证得AE∥CF,再证明AE=CF,就需证△AEB≌△CFD,即可得证。
【考点精析】通过灵活运用垂线的性质和平行四边形的判定与性质,掌握垂线的性质:1、过一点有且只有一条直线与己知直线垂直.2、垂线段最短;若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积即可以解答此题.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案科目:初中数学 来源: 题型:
【题目】如图,点A是双曲线y= ![]() (x>0)上的一动点,过A作AC⊥y轴,垂足为点C,作AC的垂直平分线交双曲线于点B,交x轴于点D.当点A在双曲线上从左到右运动时,对四边形ABCD的面积的变化情况,小明列举了四种可能:
(x>0)上的一动点,过A作AC⊥y轴,垂足为点C,作AC的垂直平分线交双曲线于点B,交x轴于点D.当点A在双曲线上从左到右运动时,对四边形ABCD的面积的变化情况,小明列举了四种可能:
①逐渐变小;
②由大变小再由小变大;
③由小变大再由大变小;
④不变.
你认为正确的是 . (填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一轮船由![]() 处向
处向![]() 处航行,在
处航行,在![]() 处测得
处测得![]() 处在
处在![]() 的北偏东
的北偏东![]() 方向上,在海岛上的观察所
方向上,在海岛上的观察所![]() 测得
测得![]() 在
在![]() 的南偏西
的南偏西![]() 方向上,
方向上,![]() 在
在![]() 的南偏东
的南偏东![]() 方向.若轮船行驶到
方向.若轮船行驶到![]() 处,那么从
处,那么从![]() 处看
处看![]() ,
,![]() 两处的视角
两处的视角![]() 是多少度?
是多少度?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,E、F分别是边AD、DC上的点,且AF⊥BE.
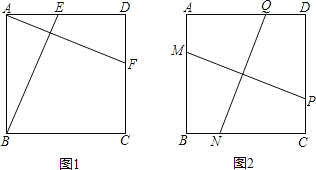
(1)求证:AF=BE;
(2)如图2,在正方形ABCD中,M、N、P、Q分别是边AB、BC、CD、DA上的点,且MP⊥NQ.MP与NQ是否相等?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
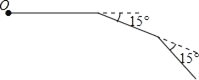
【题目】如图,小明从点O出发,前进5m后向右转15°,再前进5m后又向右转15°,…这样一直下去,直到他第一次回到出发点O为止,他所走的路径构成了一个多边形.
(1)小明一共走了多少米?
(2)这个多边形的内角和是多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC和△DBC中,∠ACB=∠DBC=90°,点E是BC的中点,EF⊥AB,垂足为F,且AB=DE.

(1)求证:△BCD是等腰直角三角形;
(2)若BD=8厘米,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解下列方程:
(1)2(10﹣0.5y)=﹣(1.5y+2)
(2)![]() (x﹣5)=3﹣
(x﹣5)=3﹣![]() (x﹣5)
(x﹣5)
(3)![]() ﹣1=
﹣1=![]()
(4)x﹣![]() (x﹣9)=
(x﹣9)=![]() [x+
[x+![]() (x﹣9)]
(x﹣9)]
(5) ![]() -
-![]() =0.5x+2
=0.5x+2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com