
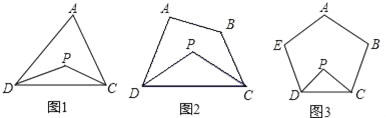
����Ŀ����1����֪����ͼ1��PΪ��ADC��һ�㣬DP��CP�ֱ�ƽ�֡�ADC�͡�ACD�������A=90������ô��P=______���������A=x�������P=____________��������ֱ���������к����ϣ�
��2����ͼ2��PΪ�ı���ABCD��һ�㣬DP��CP�ֱ�ƽ�֡�ADC�͡�BCD����̽����P���A+��B��������ϵ����д�����̽�����̣�
��3����ͼ3��PΪ�����ABCDE��һ�㣬DP��CP�ֱ�ƽ�֡�EDC�͡�BCD����ֱ��д����P���A+��B+��E��������ϵ��________________��
��4����PΪn����A1A2A3��An��һ�㣬PA1ƽ�֡�AnA1A2��PA2ƽ�֡�A1A2A3����ֱ��д����P���A3+A4+A5+����An��������ϵ��__________________________�����ú�n�Ĵ���ʽ��ʾ��
���𰸡������A=90������ô��P=135���������A=x�������P=��90+![]() ���� ��P=
���� ��P=![]() ����A+��B�� ��P=
����A+��B�� ��P=![]() ����A+��B+��E����90�� ��P=
����A+��B+��E����90�� ��P=![]() ����A3+��A4+��A5+����An������n��4����90��
����A3+��A4+��A5+����An������n��4����90��
��������
��1�����ݽ�ƽ���ߵĶ�����������ڽǺͶ�������ʽ�������
��2�����ݽ�ƽ���ߵĶ�����ı��ε��ڽǺͣ���ʽ�������
��3�����ݽ�ƽ���ߵĶ��������ε��ڽǺͣ���ʽ�������
��4�����ݽ�ƽ���ߵĶ����n���ε��ڽǺ�ʽ����ʽ�������
��1����DP��CP�ֱ�ƽ�֡�ADC�͡�ACD��
���PDC=![]() ��ADC����PCD=
��ADC����PCD=![]() ��ACD��
��ACD��
���DPC=180������PDC����PCD
=180����![]() ��ADC��
��ADC��![]() ��ACD
��ACD
=180����![]() ����ADC+��ACD��
����ADC+��ACD��
=180����![]() ��180������A��
��180������A��
=90��+ ![]() ��A��
��A��
�������A=90������ô��P=135���������A=x�������P=��90+![]() ������
������
��2����DP��CP�ֱ�ƽ�֡�ADC�͡�BCD��
���PDC=![]() ��ADC����PCD=
��ADC����PCD=![]() ��BCD��
��BCD��
���DPC=180������PDC����PCD
=180����![]() ��ADC��
��ADC��![]() ��BCD
��BCD
=180����![]() ����ADC+��BCD��
����ADC+��BCD��
=180����![]() ��360������A����B��
��360������A����B��
![]() ����A+��B����
����A+��B����
��3�������ABCDEF���ڽǺ�Ϊ����5��2��180��=540����
��DP��CP�ֱ�ƽ�֡�EDC�͡�BCD��
���PDC=![]() ��EDC����PCD=
��EDC����PCD=![]() ��BCD��
��BCD��
���P=180������PDC����PCD
=180����![]() ��EDC��
��EDC��![]() ��BCD
��BCD
=180����![]() ����EDC+��BCD��
����EDC+��BCD��
=180����![]() ��540������A����B����E��
��540������A����B����E��
=![]() ����A+��B+��E����90����
����A+��B+��E����90����
����P=![]() ����A+��B+��E����90����
����A+��B+��E����90����
��4��ͬ��1���ɵã���P=![]() ����A3+��A4+��A5+����An������n��4����90����
����A3+��A4+��A5+����An������n��4����90����
�ʴ�Ϊ����1�������A=90������ô��P=135���������A=x�������P=��90+![]() ������2����P=180������PDC����PCD=
������2����P=180������PDC����PCD=![]() ����A+��B����3����P=
����A+��B����3����P=![]() ����A+��B+��E����90����4����P=
����A+��B+��E����90����4����P=![]() ����A3+��A4+��A5+����An������n��4����90��
����A3+��A4+��A5+����An������n��4����90��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�ڽ��ڡ�O��AB�ǡ�O��ֱ������P��CA���ӳ����ϣ���CAD=45�㣮
������AB=4���� ![]() �ij���
�ij���
������ ![]() =
= ![]() ��AD=AP����֤��PD�ǡ�O�����ߣ�
��AD=AP����֤��PD�ǡ�O�����ߣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��BOC��60����OFƽ�֡�BOC.��AO��BO��OEƽ�֡�AOC�����EOF�Ķ�����(����)
A. 45��
B. 15��
C. 30����60��
D. 45����15��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����������ABCD�У�E��F�ֱ��DZ�AD��DC�ϵĵ㣬��AF��BE��
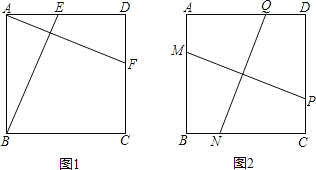
��1����֤��AF=BE��
��2����ͼ2����������ABCD�У�M��N��P��Q�ֱ��DZ�AB��BC��CD��DA�ϵĵ㣬��MP��NQ��MP��NQ�Ƿ���ȣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=��x2+2x+m��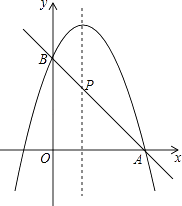
��1��������κ�����ͼ����x�����������㣬��m��ȡֵ��Χ��
��2����ͼ�����κ�����ͼ�����A��3��0������y�ύ�ڵ�B��ֱ��AB��������κ���ͼ��ĶԳ��ύ�ڵ�P�����P�����꣮
��3������ͼ��ֱ��д��ʹһ�κ���ֵ���ڶ��κ���ֵ��x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ���ڡ�ABC�͡�DBC�У���ACB=��DBC=90�㣬��E��BC���е㣬EF��AB������ΪF����AB=DE��

��1����֤����BCD�ǵ���ֱ�������Σ�
��2����BD=8���ף���AC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��ͼ1��ʾ����ij������վһ��������7���շ��������������ͼ2��ʾ����ѧ���շ�����ռ���������İٷֱ�������۲�ͼ1��ͼ2������������⣺
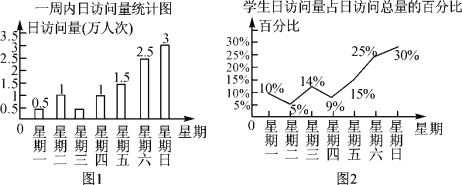
(1)����7����շ�������һ��ԼΪ10���˴Σ������������շ���������
(2)��������ѧ���շ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
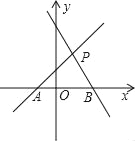
����Ŀ����ͼ��ֱ��PA��һ�κ���y��x+1��ͼ��ֱ��PB��һ�κ���y����2x+2��ͼ����
��1����A��B��P�������꣮
��2�����PAB�������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com