
【题目】如图,AB是⊙O的直径, ![]() =
= ![]() ,且AB=5,BD=4,求弦DE的长.
,且AB=5,BD=4,求弦DE的长. 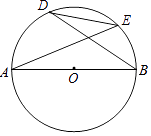
科目:初中数学 来源: 题型:
【题目】如图所示,在平行四边形ABCD中,∠ABE=∠AEB,AE∥DF,DC是∠ADF的角平分线.下列说法正确的是( )
①BE=CF ②AE是∠DAB的角平分线 ③∠DAE+∠DCF=120°.

A. ① B. ①② C. ①②③ D. 都不正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的中点,AD⊥AB交BE延长线于点D,CF平分∠ACB交BD于点F,连接CD.
求证:(1)AD=CF;
(2)点F为BD的中点.
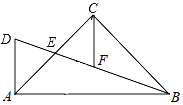
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知:如图1,P为△ADC内一点,DP、CP分别平分∠ADC和∠ACD,如果∠A=90°,那么∠P=______°;如果∠A=x°,则∠P=____________°;(答案直接填在题中横线上)
(2)如图2,P为四边形ABCD内一点,DP、CP分别平分∠ADC和∠BCD,试探究∠P与∠A+∠B的数量关系,并写出你的探索过程;
(3)如图3,P为五边形ABCDE内一点,DP、CP分别平分∠EDC和∠BCD,请直接写出∠P与∠A+∠B+∠E的数量关系:________________;
(4)若P为n边形A1A2A3…An内一点,PA1平分∠AnA1A2,PA2平分∠A1A2A3,请直接写出∠P与∠A3+A4+A5+…∠An的数量关系:__________________________.(用含n的代数式表示)
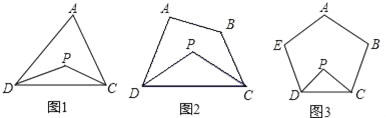
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三角形![]() 的三个项点坐标为:
的三个项点坐标为:![]() △
△![]() 内有一点
内有一点![]() 经过平移后的对应点为
经过平移后的对应点为![]() ,将△
,将△![]() 做同样平移得到△
做同样平移得到△![]() .
.

(1)写出![]() 三点的坐标:;
三点的坐标:;
(2)在图中画出△![]() ;
;
(3)求出△![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式中:
①由3x=﹣4系数化为1得x=﹣![]() ;
;
②由5=2﹣x移项得x=5﹣2;
③由![]() 去分母得2(2x﹣1)=1+3(x﹣3);
去分母得2(2x﹣1)=1+3(x﹣3);
④由2(2x﹣1)﹣3(x﹣3)=1去括号得4x﹣2﹣3x﹣9=1.
其中正确的个数有( )
A. 0个 B. 1个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前,我国大约有1.3亿高血压病患者,预防高血压不容忽视,“千帕![]() ”和“毫米汞柱
”和“毫米汞柱![]() ”都是表示血压的单位,请你根据表格提供的信息判断,下列各组换算正确的是( )
”都是表示血压的单位,请你根据表格提供的信息判断,下列各组换算正确的是( )
千帕 | … | 10 | 12 | 14 | … |
毫米汞柱 | … | 75 | 90 | 105 | … |
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列解题过程的空白处填上适当的内容(推理的理由或数据).
如图,![]() ,
,![]() ,
,![]() ,那么
,那么![]() 吗?说明理由.
吗?说明理由.
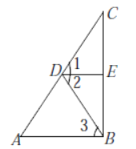
解:![]() ,理由如下:
,理由如下:
因为![]() ,
,![]() (已知)
(已知)
所以![]()
所以![]() (__________________
(__________________![]() ).
).
所以![]() (_________________________________).
(_________________________________).
所以![]() (__________________________________).
(__________________________________).
![]() (______________________________________).
(______________________________________).
因为![]() ,
,
所以![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com