
【题目】已知二次函数y=﹣x2+2x+m.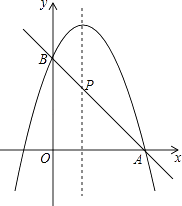
(1)如果二次函数的图象与x轴有两个交点,求m的取值范围;
(2)如图,二次函数的图象过点A(3,0),与y轴交于点B,直线AB与这个二次函数图象的对称轴交于点P,求点P的坐标.
(3)根据图象直接写出使一次函数值大于二次函数值的x的取值范围.
【答案】
(1)解:∵二次函数的图象与x轴有两个交点,
∴△=22+4m>0
∴m>﹣1;
(2)解:∵二次函数的图象过点A(3,0),
∴0=﹣9+6+m
∴m=3,
∴二次函数的解析式为:y=﹣x2+2x+3,
令x=0,则y=3,
∴B(0,3),
设直线AB的解析式为:y=kx+b,
∴ ![]() ,解得:
,解得: ![]() ,
,
∴直线AB的解析式为:y=﹣x+3,
∵抛物线y=﹣x2+2x+3,的对称轴为:x=1,
∴把x=1代入y=﹣x+3得y=2,
∴P(1,2).
(3)解:根据函数图象可知:x<0或x>3.
【解析】(1)根据已知二次函数的图象与x轴有两个交点,可得b2-4ac>0,建立不等式,求解即可。
(2)利用待定系数法,根据点A的坐标即可求出此抛物线的函数解析式,再由y=0,求出抛物线与y轴的交点坐标,再利用待定系数法求出直线AB的解析式,然后将抛物线和一次函数联立解方程组即可求得点P的坐标。
(3)观察函数图像,使一次函数值大于二次函数值,就是看一次函数图像高于二次函数的图像,即可得出x的取值范围。
【考点精析】关于本题考查的确定一次函数的表达式和抛物线与坐标轴的交点,需要了解确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.才能得出正确答案.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
【题目】如图,将两张长为4,宽为1的矩形纸条交叉并旋转,使重叠部分成为一个菱形.旋转过程中,当两张纸条垂直时,菱形周长的最小值是4,那么菱形周长的最大值是 . 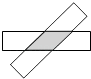
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】形如半圆型的量角器直径为4cm,放在如图所示的平面直角坐标系中(量角器的中心与坐标原点O重合,零刻度线在x轴上),连接60°和120°刻度线的一个端点P、Q,线段PQ交y轴于点A,则点A的坐标为( ) 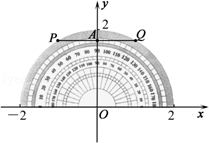
A.(﹣1, ![]() )
)
B.(0, ![]() )
)
C.( ![]() ,0)
,0)
D.(1, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
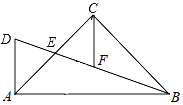
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的中点,AD⊥AB交BE延长线于点D,CF平分∠ACB交BD于点F,连接CD.
求证:(1)AD=CF;
(2)点F为BD的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的内角∠BAD、∠CDA的角平分线交于点E,∠ABC、∠BCD的角平分线交于点F.
(1)若∠F=70°,则∠ABC+∠BCD= ______ °;∠E= ______ °;
(2)探索∠E与∠F有怎样的数量关系,并说明理由;
(3)给四边形ABCD添加一个条件,使得∠E=∠F,所添加的条件为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
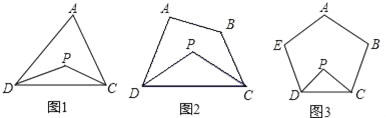
【题目】(1)已知:如图1,P为△ADC内一点,DP、CP分别平分∠ADC和∠ACD,如果∠A=90°,那么∠P=______°;如果∠A=x°,则∠P=____________°;(答案直接填在题中横线上)
(2)如图2,P为四边形ABCD内一点,DP、CP分别平分∠ADC和∠BCD,试探究∠P与∠A+∠B的数量关系,并写出你的探索过程;
(3)如图3,P为五边形ABCDE内一点,DP、CP分别平分∠EDC和∠BCD,请直接写出∠P与∠A+∠B+∠E的数量关系:________________;
(4)若P为n边形A1A2A3…An内一点,PA1平分∠AnA1A2,PA2平分∠A1A2A3,请直接写出∠P与∠A3+A4+A5+…∠An的数量关系:__________________________.(用含n的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三角形![]() 的三个项点坐标为:
的三个项点坐标为:![]() △
△![]() 内有一点
内有一点![]() 经过平移后的对应点为
经过平移后的对应点为![]() ,将△
,将△![]() 做同样平移得到△
做同样平移得到△![]() .
.

(1)写出![]() 三点的坐标:;
三点的坐标:;
(2)在图中画出△![]() ;
;
(3)求出△![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前,我国大约有1.3亿高血压病患者,预防高血压不容忽视,“千帕![]() ”和“毫米汞柱
”和“毫米汞柱![]() ”都是表示血压的单位,请你根据表格提供的信息判断,下列各组换算正确的是( )
”都是表示血压的单位,请你根据表格提供的信息判断,下列各组换算正确的是( )
千帕 | … | 10 | 12 | 14 | … |
毫米汞柱 | … | 75 | 90 | 105 | … |
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】仔细阅读下面例题,解答问题
例题:已知二次三项式x2﹣4x+m有一个因式是(x+3),求另一个因式以及m的值.
解:设另一个因式为(x+n),得x2﹣4x+m=(x+3)(x+n),
则x2﹣4x+m=x2+(n+3)x+3n
∴![]()
解得:n=﹣7,m=﹣21.
∴另一个因式为(x﹣7),m的值为﹣21.
问题:
(1)若二次三项式x2﹣5x+6可分解为(x﹣2)(x+a),则a= ;
(2)若二次三项式2x2+bx﹣5可分解为(2x﹣1)(x+5),则b= ;
(3)仿照以上方法解答下面问题:若二次三项式2x2+3x﹣k有一个因式是(2x﹣5),求另一个因式以及k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com