
【题目】某种产品的年产量不超过1 000t,该产品的年产量(t)与费用(万元)之间的函数关系如图(1);该产品的年销售量(t)与每吨销售价(万元)之间的函数关系如图(2).若生产出的产品都能在当年销售完,则年产量为多少吨时,当年可获得7500万元毛利润?(毛利润=销售额﹣费用)
【答案】解:设年产量为t吨,费用为y(万元),每吨销售价为z(万元),则0≤t≤1000,
由图(1)可求得y=10t,
由图(2)求得z=﹣ ![]() t+30.
t+30.
设毛利润为w(万元),
则w=tz﹣y=t(﹣ ![]() t+30)﹣10t=﹣
t+30)﹣10t=﹣ ![]() t2+20t.
t2+20t.
∴﹣ ![]() t2+20t=7500,
t2+20t=7500,
∴t2﹣2000t+750000=0,
解得t1=500,t2=1500(不合题意,舍去).
故年产量是500吨时,当年可获得7500万元毛利润.
【解析】(1)先观察函数图像,根据图像上的点的坐标,利用待定系数法求出两函数的解析式。然后设毛利润为w(万元),根据毛利润=销售额﹣费用。得出w=tz﹣y,列出w与t的函数关系式,根据w=7500,建立方程求解,再根据某种产品的年产量不超过1 000吨,得出t的值。,


科目:初中数学 来源: 题型:
【题目】某校七年级为了开展球类兴趣小组,需要购买一批足球和篮球﹒若购买3个足球和5个篮球需580元;若购买4个足球和3个篮球需480元.
(1)求出足球和篮球的的单价分别是多少?
(2)已知该年级决定用800元购进这两种球,若两种球都要有,请问有几种购买方案,并请加以说明﹒
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=30°,以直角边AB为直径作半圆交AC于点D,以AD为边作等边△ADE,延长ED交BC于点F,BC=2 ![]() ,则图中阴影部分的面积为 . (结果不取近似值)
,则图中阴影部分的面积为 . (结果不取近似值) 
查看答案和解析>>
科目:初中数学 来源: 题型:
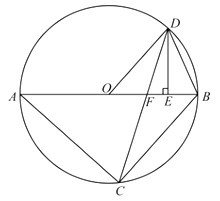
【题目】如图,已知 ![]() 内接于
内接于 ![]() ,
, ![]() 是直径,点
是直径,点 ![]() 在
在 ![]() 上,
上, ![]() ,过点
,过点 ![]() 作
作 ![]() ,垂足为
,垂足为 ![]() ,连接
,连接 ![]() 交
交 ![]() 边于点
边于点 ![]() .
.
(1)求证: ![]() ∽
∽ ![]() ;
;
(2)求证: ![]() ;
;
(3)连接 ![]() ,设
,设 ![]() 的面积为
的面积为 ![]() ,四边形
,四边形 ![]() 的面积为
的面积为 ![]() ,若
,若 ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平行四边形ABCD中,∠ABE=∠AEB,AE∥DF,DC是∠ADF的角平分线.下列说法正确的是( )
①BE=CF ②AE是∠DAB的角平分线 ③∠DAE+∠DCF=120°.

A. ① B. ①② C. ①②③ D. 都不正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<6),连接DE,当△BDE是直角三角形时,t的值为( )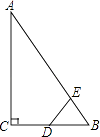
A.2
B.2.5或3.5
C.3.5或4.5
D.2或3.5或4.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一块长方形场地ABCD的长AB与宽AD的比为2∶1,DE⊥AC于点E,BF⊥AC于点F,连结BE,DF,则四边形DEBF与长方形ABCD的面积比为__________.
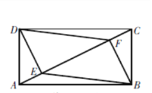
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式中:
①由3x=﹣4系数化为1得x=﹣![]() ;
;
②由5=2﹣x移项得x=5﹣2;
③由![]() 去分母得2(2x﹣1)=1+3(x﹣3);
去分母得2(2x﹣1)=1+3(x﹣3);
④由2(2x﹣1)﹣3(x﹣3)=1去括号得4x﹣2﹣3x﹣9=1.
其中正确的个数有( )
A. 0个 B. 1个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com