
【题目】如图,已知 ![]() 内接于
内接于 ![]() ,
, ![]() 是直径,点
是直径,点 ![]() 在
在 ![]() 上,
上, ![]() ,过点
,过点 ![]() 作
作 ![]() ,垂足为
,垂足为 ![]() ,连接
,连接 ![]() 交
交 ![]() 边于点
边于点 ![]() .
.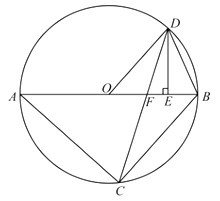
(1)求证: ![]() ∽
∽ ![]() ;
;
(2)求证: ![]() ;
;
(3)连接 ![]() ,设
,设 ![]() 的面积为
的面积为 ![]() ,四边形
,四边形 ![]() 的面积为
的面积为 ![]() ,若
,若 ![]() ,求
,求 ![]() 的值.
的值.
【答案】
(1)
证明:∵AB是圆O的直径,
∴∠ACB=90°,
∵DE⊥AB,
∴∠DEO=90°,
∴∠DEO=∠ACB,
∵OD//BC,
∴∠DOE=∠ABC,
∴△DOE~△ABC,
(2)
证明:∵△DOE~△ABC,
∴∠ODE=∠A,
∵∠A和∠BDC是弧BC所对的圆周角,
∴∠A=∠BDC,
∴∠ODE=∠BDC,
∴∠ODF=∠BDE。
(3)
解:因为△DOE~△ABC ,
所以![]() ,
,
即![]() =4
=4![]() =4
=4![]()
因为OA=OB,
所以![]() =
=![]() ,即
,即![]() =2
=2![]() ,
,
因为![]() =
=![]() ,S2=
,S2=![]() +
+![]() +
+![]() =2S1+S1+
=2S1+S1+![]() ,
,
所以![]() =
=![]() ,
,
所以BE=![]() OE,即OE=
OE,即OE=![]() OB=
OB=![]() OD,
OD,
所以sinA=sin∠ODE=![]() =
=![]()
【解析】(1)易证∠DEO=∠ACB=90°和∠DOE=∠ABC,根据“有两对角相等的两个三角形相似”判定△DOE~△ABC;
(2)由△DOE~△ABC,可得∠ODE=∠A,由∠A和∠BDC是弧BC所对的圆周角,则∠A=∠BDC,从而通过角的等量代换即可证得;
(3)由∠ODE=∠A,可得sinA=sin∠ODE=![]() =
=![]() ;而由△DOE~△ABC ,可得
;而由△DOE~△ABC ,可得![]() , 即
, 即![]() =4
=4![]() =4
=4![]()
![]() =
=![]() , 即
, 即![]() =2
=2![]() ,又因为
,又因为![]() =
=![]() ,S2=
,S2=![]() +
+![]() +
+![]() =2S1+S1+
=2S1+S1+![]() ,则可得
,则可得![]() =
=![]() , 可求得OE与OB的比值.
, 可求得OE与OB的比值.
【考点精析】认真审题,首先需要了解圆周角定理(顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半),还要掌握相似三角形的性质(对应角相等,对应边成比例的两个三角形叫做相似三角形)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
【题目】观察下列等式:
① ![]() +
+ ![]() ﹣
﹣ ![]() =
= ![]() ;
;
② ![]() +
+ ![]() ﹣
﹣ ![]() =
= ![]() ;
;
③ ![]() +
+ ![]() ﹣
﹣ ![]() =
= ![]() ;
;
④ ![]() +
+ ![]() ﹣
﹣ ![]() =
= ![]() ;
;
…
(1)请按以上规律写出第⑤个等式:;
(2)猜想并写出第n个等式:;
(3)请证明猜想的正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
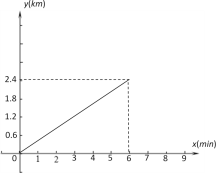
【题目】已知A、B两地相距2.4km,甲骑车匀速从A地前往B地,如图表示甲骑车过程中离A地的路程y(km)与他行驶所用的时间x(min)之间的关系.根据图像解答下列问题:
(1)甲骑车的速度是 km/min;
(2)若在甲出发时,乙在甲前方0.6km处,两人均沿同一路线同时出发匀速前往B地,在第3分钟甲追上了乙,两人到达B地后停止.请在下面同一平面直角坐标系中画出乙离A地的距离y乙(km)与所用时间x(min)的关系的大致图像;
(3)乙在第几分钟到达B地?
(4)两人在整个行驶过程中,何时相距0.2km?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是双曲线y= ![]() (x>0)上的一动点,过A作AC⊥y轴,垂足为点C,作AC的垂直平分线交双曲线于点B,交x轴于点D.当点A在双曲线上从左到右运动时,对四边形ABCD的面积的变化情况,小明列举了四种可能:
(x>0)上的一动点,过A作AC⊥y轴,垂足为点C,作AC的垂直平分线交双曲线于点B,交x轴于点D.当点A在双曲线上从左到右运动时,对四边形ABCD的面积的变化情况,小明列举了四种可能:
①逐渐变小;
②由大变小再由小变大;
③由小变大再由大变小;
④不变.
你认为正确的是 . (填序号)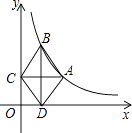
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,AB是⊙O的直径,点P在CA的延长线上,∠CAD=45°.
(Ⅰ)若AB=4,求 ![]() 的长;
的长;
(Ⅱ)若 ![]() =
= ![]() ,AD=AP,求证:PD是⊙O的切线.
,AD=AP,求证:PD是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种产品的年产量不超过1 000t,该产品的年产量(t)与费用(万元)之间的函数关系如图(1);该产品的年销售量(t)与每吨销售价(万元)之间的函数关系如图(2).若生产出的产品都能在当年销售完,则年产量为多少吨时,当年可获得7500万元毛利润?(毛利润=销售额﹣费用)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一轮船由![]() 处向
处向![]() 处航行,在
处航行,在![]() 处测得
处测得![]() 处在
处在![]() 的北偏东
的北偏东![]() 方向上,在海岛上的观察所
方向上,在海岛上的观察所![]() 测得
测得![]() 在
在![]() 的南偏西
的南偏西![]() 方向上,
方向上,![]() 在
在![]() 的南偏东
的南偏东![]() 方向.若轮船行驶到
方向.若轮船行驶到![]() 处,那么从
处,那么从![]() 处看
处看![]() ,
,![]() 两处的视角
两处的视角![]() 是多少度?
是多少度?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC和△DBC中,∠ACB=∠DBC=90°,点E是BC的中点,EF⊥AB,垂足为F,且AB=DE.

(1)求证:△BCD是等腰直角三角形;
(2)若BD=8厘米,求AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com