
【题目】如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<6),连接DE,当△BDE是直角三角形时,t的值为( )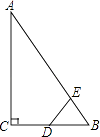
A.2
B.2.5或3.5
C.3.5或4.5
D.2或3.5或4.5
【答案】D
【解析】解:∵Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,
∴AB=2BC=4(cm),
∵BC=2cm,D为BC的中点,动点E以1cm/s的速度从A点出发,
∴BD= ![]() BC=1(cm),BE=AB﹣AE=4﹣t(cm),
BC=1(cm),BE=AB﹣AE=4﹣t(cm),
若∠BED=90°,
当A→B时,∵∠ABC=60°,
∴∠BDE=30°,
∴BE= ![]() BD=
BD= ![]() (cm),
(cm),
∴t=3.5,
当B→A时,t=4+0.5=4.5.
若∠BDE=90°时,
当A→B时,∵∠ABC=60°,
∴∠BED=30°,
∴BE=2BD=2(cm),
∴t=4﹣2=2,
当B→A时,t=4+2=6(舍去).
综上可得:t的值为2或3.5或4.5.
所以答案是:D.
【考点精析】本题主要考查了含30度角的直角三角形和勾股定理的概念的相关知识点,需要掌握在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某厂计划生产A、B两种产品共50件.已知A产品每件可获利润1200元,B产品每件可获利润700元,设生产两种产品的获利总额为y(元),生产A产品x(件).
(1)写出y与x之间的函数关系式;
(2)若生产A、B两种产品的件数均不少于10件,求总利润的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是双曲线y= ![]() (x>0)上的一动点,过A作AC⊥y轴,垂足为点C,作AC的垂直平分线交双曲线于点B,交x轴于点D.当点A在双曲线上从左到右运动时,对四边形ABCD的面积的变化情况,小明列举了四种可能:
(x>0)上的一动点,过A作AC⊥y轴,垂足为点C,作AC的垂直平分线交双曲线于点B,交x轴于点D.当点A在双曲线上从左到右运动时,对四边形ABCD的面积的变化情况,小明列举了四种可能:
①逐渐变小;
②由大变小再由小变大;
③由小变大再由大变小;
④不变.
你认为正确的是 . (填序号)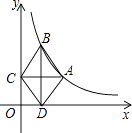
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种产品的年产量不超过1 000t,该产品的年产量(t)与费用(万元)之间的函数关系如图(1);该产品的年销售量(t)与每吨销售价(万元)之间的函数关系如图(2).若生产出的产品都能在当年销售完,则年产量为多少吨时,当年可获得7500万元毛利润?(毛利润=销售额﹣费用)
查看答案和解析>>
科目:初中数学 来源: 题型:
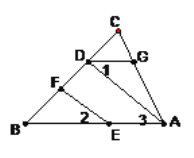
【题目】(7分)如图,EF//AD, ![]() =
=![]() .求证:∠DGA+∠BAC=180°.请将说明过程填写完成.
.求证:∠DGA+∠BAC=180°.请将说明过程填写完成.
证明:∵EF//AD,(已知)
∴![]() =_____(_____________________________).
=_____(_____________________________).
又∵![]() =
=![]() (______)
(______)
∴![]() =
=![]() (________________________).
(________________________).
∴AB//______(____________________________)
∴∠DGA+∠BAC=180°(_____________________________)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一轮船由![]() 处向
处向![]() 处航行,在
处航行,在![]() 处测得
处测得![]() 处在
处在![]() 的北偏东
的北偏东![]() 方向上,在海岛上的观察所
方向上,在海岛上的观察所![]() 测得
测得![]() 在
在![]() 的南偏西
的南偏西![]() 方向上,
方向上,![]() 在
在![]() 的南偏东
的南偏东![]() 方向.若轮船行驶到
方向.若轮船行驶到![]() 处,那么从
处,那么从![]() 处看
处看![]() ,
,![]() 两处的视角
两处的视角![]() 是多少度?
是多少度?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解下列方程:
(1)2(10﹣0.5y)=﹣(1.5y+2)
(2)![]() (x﹣5)=3﹣
(x﹣5)=3﹣![]() (x﹣5)
(x﹣5)
(3)![]() ﹣1=
﹣1=![]()
(4)x﹣![]() (x﹣9)=
(x﹣9)=![]() [x+
[x+![]() (x﹣9)]
(x﹣9)]
(5) ![]() -
-![]() =0.5x+2
=0.5x+2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com