
【题目】某厂计划生产A、B两种产品共50件.已知A产品每件可获利润1200元,B产品每件可获利润700元,设生产两种产品的获利总额为y(元),生产A产品x(件).
(1)写出y与x之间的函数关系式;
(2)若生产A、B两种产品的件数均不少于10件,求总利润的最大值.
【答案】(1) y=500 x+35000;(2)55000元.
【解析】
(1)首先表示出B种产品的数量进而利用A,B种产品的利润进而得出总利润;(2)利用不等式组求出x的取值范围,进而利用一次函数增减性进而得出最大利润.
本题解析:
(1)设生产两种产品的获利总额为y(元),生产A产品x(件),则B种产品共(50-x)件,
∴y与x之间的函数关系式为:y=1200x+700(50-x)=500 x+35000;
(2)∵生产A、B两种产品的件数均不少于10件,
∴![]() ,
,
解得:10≤x≤40,
∵y=500x+35000,y随x的增大而增大,
∴当x=40时,此时达到总利润的最大值为:40×500+35000=55000(元),
答:总利润的最大值为55000元.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】某体育文化用品商店购进篮球和排球共30个,进价和售价如下表,若全部销售完后共可获利润1680元.
篮球 | 排球 | |
进价(元/个) | 150 | 120 |
售价(元/个) | 200 | 180 |
(1)请利用二元一次方程组求购进篮球和排球各多少个?
(2)“双11”快到了,这个体育文化用品商店也准备搞促销活动,计划篮球9折销售,排球8折销售,则销售8个篮球的利润与销售几个排球的利润相等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=BC,BD⊥AC于点D. 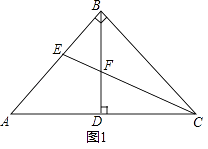
(1)如图1,当∠ABC=90°时,若CE平分∠ACB,交AB于点E,交BD于点F. ①求证:△BEF是等腰三角形;
②求证:BD= ![]() (BC+BF);
(BC+BF);
(2)点E在AB边上,连接CE.若BD= ![]() (BC+BE),在图2中补全图形,判断∠ACE与∠ABC之间的数量关系,写出你的结论,并写出求解∠ACE与∠ABC关系的思路.
(BC+BE),在图2中补全图形,判断∠ACE与∠ABC之间的数量关系,写出你的结论,并写出求解∠ACE与∠ABC关系的思路. 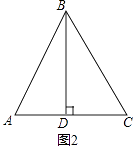
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() ,
,![]() .试说明直线
.试说明直线![]() 与
与![]() 垂直.(请在下面的解答过程的空格内填空或在括号内填写理由).
垂直.(请在下面的解答过程的空格内填空或在括号内填写理由).

理由:![]() ,(已知)
,(已知)
![]()
![]() ,
,![]()
![]()
![]() .
.![]()
![]()
又![]() ,(已知)
,(已知)
![]()
![]() .(等量代换)
.(等量代换)
![]()
![]() ,
,![]()
![]()
![]() .
.![]()
![]()
![]() ,(已知)
,(已知)
![]() ,
,![]() ,
,
![]()
![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+8(a≠0)与x轴交于A(﹣2,0),B两点,与y轴交于C点,tan∠ABC=2. 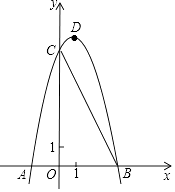
(1)求抛物线的表达式及其顶点D的坐标;
(2)过点A、B作x轴的垂线,交直线CD于点E、F,将抛物线沿其对称轴向上平移m个单位,使抛物线与线段EF(含线段端点)只有1个公共点.求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年9月17日世界人工智能大会在上海召开,人工智能的变革力在教育、制造等领域加速落地. 在某市举办的一次中学生机器人足球赛中,有四个代表队进入决赛,决赛中,每个队分别与其它三个队进行主客场比赛各一场(即每个队要进行6场比赛),以下是积分表的一部分.
排名 | 代表队 | 场次 (场) | 胜 (场) | 平 (场) | 负 (场) | 净胜球 (个) | 进球 (个) | 失球 (个) | 积分 (分) |
1 | A | 6 | 1 | 6 | 12 | 6 | 22 | ||
2 | B | 6 | 3 | 2 | 1 | 0 | 6 | 6 | 19 |
3 | C | 6 | 3 | 1 | 2 | 2 | 9 | 7 | 17 |
4 | D | 6 | 0 | 0 | 6 | m | 5 | 13 | 0 |
(说明:积分=胜场积分+平场积分+负场积分)
(1)D代表队的净胜球数m= ;
(2)本次决赛中,胜一场积 分,平一场积 分,负一场积 分;
(3)此次竞赛的奖金分配方案为:进入决赛的每支代表队都可以获得参赛奖金6000元;另外,在决赛期间,每胜一场可以再获得奖金2000元,每平一场再获得奖金1000元.
请根据表格提供的信息,求出冠军A队一共能获得多少奖金.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知直线l1:y=mx(m≠0)与直线l2:y=ax+b(a≠0)相交于点A(1,2),直线l2与x轴交于点B(3,0).
(1)分别求直线l1和l2的表达式;
(2)过动点P(0,n)且平行于x轴的直线与l1 , l2的交点分别为C,D,当点C位于点D左方时,写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆的直径,点D是弧AC的中点,∠B=50°,则下列判断不正确的是( ) 
A.∠ACB=90°
B.AC=2CD
C.∠DAB=65°
D.∠DAB+∠DCB=180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的顶点A,C落在坐标轴上,且顶点B的坐标为(﹣5,2),将△ABC沿x轴向右平移得到△A1B1C1 , 使得点B1恰好落在函数y= ![]() 上,若线段AC扫过的面积为48,则点C1的坐标为( )
上,若线段AC扫过的面积为48,则点C1的坐标为( ) 
A.(3,2)
B.(5,6)
C.(8,6)
D.(6,6)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com