
【题目】在△ABC中,AB=BC,BD⊥AC于点D. 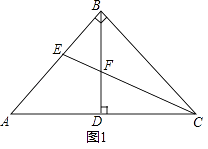
(1)如图1,当∠ABC=90°时,若CE平分∠ACB,交AB于点E,交BD于点F. ①求证:△BEF是等腰三角形;
②求证:BD= ![]() (BC+BF);
(BC+BF);
(2)点E在AB边上,连接CE.若BD= ![]() (BC+BE),在图2中补全图形,判断∠ACE与∠ABC之间的数量关系,写出你的结论,并写出求解∠ACE与∠ABC关系的思路.
(BC+BE),在图2中补全图形,判断∠ACE与∠ABC之间的数量关系,写出你的结论,并写出求解∠ACE与∠ABC关系的思路. 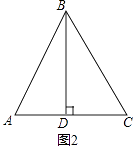
【答案】
(1)解:①在△ABC中,AB=BC,BD⊥AC于点D,
∴∠ABD=∠CBD,AD=CD,
∵∠ABC=90°,
∴∠ACB=45°,
∵CE平分∠ACB,
∴∠ECB=∠ACE=22.5°,
∴∠BEF=∠CFD=∠BFE=67.5°,
∴BE=BF,
∴△BEF是等腰三角形;
②如图,延长AB至M,使得BM=AB,连接CM,
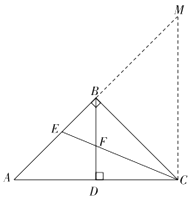
∴BD∥CM,BD= ![]() CM,
CM,
∴∠BCM=∠DBC=∠ABD=∠BMC=45°,
∠BFE=∠MCE,
∴BC=BM,
由①得,∠BEF=∠BFE,BE=BF,
∴∠BFE=∠MCE=∠BEF,
∴EM=MC,
∴BD= ![]() EM=
EM= ![]() (BC+BF)
(BC+BF)
(2)解:∠ACE= ![]() ∠ABC.
∠ABC.

求解∠ACE与∠ABC关系的思路:
a,延长AB至P,使得BP=AB,连接CP,与(1)②同理可得BD∥PC,BD= ![]() PC,BP=BC;
PC,BP=BC;
b,由BD= ![]() (BC+BE),可证明△PEC和△BEF分别是等腰三角形;
(BC+BE),可证明△PEC和△BEF分别是等腰三角形;
c,由∠BEF+∠BFE+∠EBF=180°以及∠FCD+∠DFC=90°,可得 ![]() =90°﹣∠DCF,即可证明∠ACE=
=90°﹣∠DCF,即可证明∠ACE= ![]() ∠ABC.
∠ABC.
【解析】(1)①根据∠ABC=90°,∠FDC=90°,以及∠ECB=∠ACE=22.5°,即可得到∠BEF=∠CFD=∠BFE=67.5°,即可判定△BEF是等腰三角形;②延长AB至M,使得BM=AB,连接CM,根据三角形中位线定理可得BD∥CM,BD= ![]() CM,再根据∠BFE=∠MCE=∠BEF,可得EM=MC,进而得出BD=
CM,再根据∠BFE=∠MCE=∠BEF,可得EM=MC,进而得出BD= ![]() EM=
EM= ![]() (BC+BF);(2)与(1)②同理可得BD∥PC,BD=
(BC+BF);(2)与(1)②同理可得BD∥PC,BD= ![]() PC,BP=BC;由BD=
PC,BP=BC;由BD= ![]() (BC+BE),可证明△PEC和△BEF分别是等腰三角形;由∠BEF+∠BFE+∠EBF=180°以及∠FCD+∠DFC=90°,可得
(BC+BE),可证明△PEC和△BEF分别是等腰三角形;由∠BEF+∠BFE+∠EBF=180°以及∠FCD+∠DFC=90°,可得 ![]() =90°﹣∠DCF,即可得到∠ACE与∠ABC之间的数量关系:∠ACE=
=90°﹣∠DCF,即可得到∠ACE与∠ABC之间的数量关系:∠ACE= ![]() ∠ABC.
∠ABC.
【考点精析】解答此题的关键在于理解等腰直角三角形的相关知识,掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°.


科目:初中数学 来源: 题型:
【题目】如图,AB与CD交于点O,OE平分∠AOC,点F为AB上一点(不与点A及O重合),过点F作FG∥OE,交CD于点G,若∠AOD=110°,则∠AFG度数为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,对角线BD平分∠ABC,过点A作AE∥BD,交CD的延长线于点E,过点E作EF⊥BC,交BC延长线于点F. 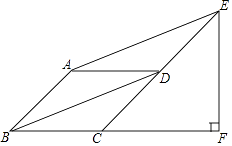
(1)求证:四边形ABCD是菱形;
(2)若∠ABC=45°,BC=2,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(探究)如图①,∠AFH和∠CHF的平分线交于点O,EG经过点O且平行于FH,分别与AB、CD交于点E、G.
(1)若∠AFH=60°,∠CHF=50°,则∠EOF=_____度,∠FOH=_____度.
(2)若∠AFH+∠CHF=100°,求∠FOH的度数.
(拓展)如图②,∠AFH和∠CHI的平分线交于点O,EG经过点O且平行于FH,分别与AB、CD交于点E、G.若∠AFH+∠CHF=α,直接写出∠FOH的度数.(用含a的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.
(1)试判断直线AB与直线CD的位置关系,并说明理由;
(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;
(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,问∠HPQ的大小是否发生变化?若不变,请求出其值;若变化,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料: 在数学课上,老师提出如下问题:
已知:如图,四边形ABCD是平行四边形.求作:菱形AECF,使点E,F分别在BC,AD上.
小凯的作法如下:
(i)连接AC;
(ii)作AC的垂直平分线EF分别交BC,AD于E,F;
(iii)连接AE,CF.
所以四边形AECF是菱形.
老师说:“小凯的作法正确.”
请回答:在小凯的作法中,判定四边形AECF是菱形的依据是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,AB=2,BC=1,运点P从点B出发,沿路线B![]() C
C![]() D作匀速运动,那么△ABP的面积
D作匀速运动,那么△ABP的面积![]() 与点P运动的路程之间的函数图象大致是( ).
与点P运动的路程之间的函数图象大致是( ).

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂计划生产A、B两种产品共50件.已知A产品每件可获利润1200元,B产品每件可获利润700元,设生产两种产品的获利总额为y(元),生产A产品x(件).
(1)写出y与x之间的函数关系式;
(2)若生产A、B两种产品的件数均不少于10件,求总利润的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知CD、BF相交于点O,∠D=![]() ,下面判定两直线平行正确的是( )
,下面判定两直线平行正确的是( )

A. 当∠C=![]() 时,AB∥CD B. 当∠A=
时,AB∥CD B. 当∠A=![]() 时,AC∥DE
时,AC∥DE
C. 当∠E=![]() 时,CD∥EF D. 当∠BOC=
时,CD∥EF D. 当∠BOC=![]() 时,BF∥DE
时,BF∥DE
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com