
【题目】如图,在ABCD中,对角线BD平分∠ABC,过点A作AE∥BD,交CD的延长线于点E,过点E作EF⊥BC,交BC延长线于点F. 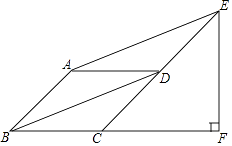
(1)求证:四边形ABCD是菱形;
(2)若∠ABC=45°,BC=2,求EF的长.
【答案】
(1)解:证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,AB∥CD,
∴∠ADB=∠CBD,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∴∠ADB=∠ABD,
∴AB=AD,
∴ABCD是菱形
(2)解:∵四边形ABCD是菱形,
∴AB=CD=BC=2,
∵AB∥CD,AE∥BD,
∴四边形ABDE是平行四边形,∠ECF=∠ABC=45°,
∴AB=DE=2,
∴CE=CD+DE=4,
∵EF⊥BC,∠ECF=45°,
∴△CEF是等腰直角三角形,
∴EF=CF= ![]() CE=2
CE=2 ![]()
【解析】(1)证明∠ADB=∠ABD,得出AB=AD,即可得出结论;(2)由菱形的性质得出AB=CD=BC=2,证明四边形ABDE是平行四边形,∠ECF=∠ABC=45°,得出AB=DE=2,CE=CD+DE=4,在Rt△CEF中,由等腰直角三角形的性质和勾股定理即可求出EF的长.
【考点精析】根据题目的已知条件,利用平行四边形的性质的相关知识可以得到问题的答案,需要掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:
【题目】如图,∠AOB=45°,点M,N在边OA上,OM=x,ON=x+4,点P是边OB上的点.若使点P,M,N构成等腰三角形的点P恰好有三个,则x的值是.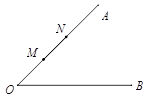
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育文化用品商店购进篮球和排球共30个,进价和售价如下表,若全部销售完后共可获利润1680元.
篮球 | 排球 | |
进价(元/个) | 150 | 120 |
售价(元/个) | 200 | 180 |
(1)请利用二元一次方程组求购进篮球和排球各多少个?
(2)“双11”快到了,这个体育文化用品商店也准备搞促销活动,计划篮球9折销售,排球8折销售,则销售8个篮球的利润与销售几个排球的利润相等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下列推理过程:
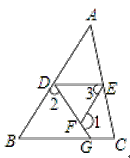
已知:如图,∠1+∠2=180°,∠3=∠B
求证:∠EDG+∠DGC=180°
证明:∵∠1+∠2=180°(已知)
∠1+∠DFE=180°( )
∴∠2= ( )
∴EF∥AB( )
∴∠3= ( )
又∵∠3=∠B(已知)
∴∠B=∠ADE( )
∴DE∥BC( )
∴∠EDG+∠DGC=180°( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】汽车保有量是指一个地区拥有车辆的数量,一般是指在当地登记的车辆.进入21世纪以来,我国汽车保有量逐年增长.如图是根据中国产业信息网上的有关数据整理的统计图. 2007﹣2015年全国汽车保有量及增速统计图,
根据以上信息,回答下列问题:
(1)2016年汽车保有量净增2200万辆,为历史最高水平,2016年汽车的保有量为万辆,与2015年相比,2016年的增长率约为%;
(2)从2008年到2015年,年全国汽车保有量增速最快;
(3)预估2020年我国汽车保有量将达到万辆,预估理由是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C为⊙O上一点,过点C作⊙O的切线,交BA的延长线交于点D,过点B作BE⊥BA,交DC延长线于点E,连接OE,交⊙O于点F,交BC于点H,连接AC. 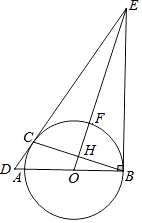
(1)求证:∠ECB=∠EBC;
(2)连接BF,CF,若CF=6,sin∠FCB= ![]() ,求AC的长.
,求AC的长. 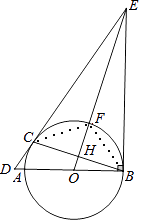
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=BC,BD⊥AC于点D. 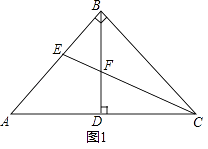
(1)如图1,当∠ABC=90°时,若CE平分∠ACB,交AB于点E,交BD于点F. ①求证:△BEF是等腰三角形;
②求证:BD= ![]() (BC+BF);
(BC+BF);
(2)点E在AB边上,连接CE.若BD= ![]() (BC+BE),在图2中补全图形,判断∠ACE与∠ABC之间的数量关系,写出你的结论,并写出求解∠ACE与∠ABC关系的思路.
(BC+BE),在图2中补全图形,判断∠ACE与∠ABC之间的数量关系,写出你的结论,并写出求解∠ACE与∠ABC关系的思路. 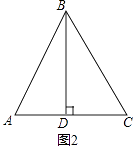
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知直线l1:y=mx(m≠0)与直线l2:y=ax+b(a≠0)相交于点A(1,2),直线l2与x轴交于点B(3,0).
(1)分别求直线l1和l2的表达式;
(2)过动点P(0,n)且平行于x轴的直线与l1 , l2的交点分别为C,D,当点C位于点D左方时,写出n的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com