
【题目】如图,∠AOB=45°,点M,N在边OA上,OM=x,ON=x+4,点P是边OB上的点.若使点P,M,N构成等腰三角形的点P恰好有三个,则x的值是.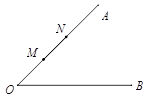
【答案】x=0或x= ![]() 或4≤x<4
或4≤x<4 ![]()
【解析】解:以MN为底边时,可作MN的垂直平分线,与OB必有一个交点P1 , 且MN=4,以M为圆心MN为半径画圆,以N为圆心MN为半径画圆,
①如下图,当M与点O重合时,即x=0时,
除了P1 , 当MN=MP,即为P3;当NP=MN时,即为P2;
只有3个点P;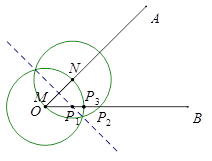
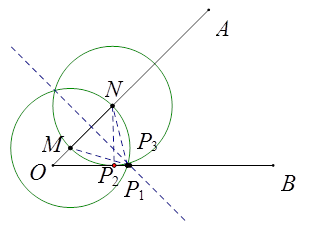
②当0<x<4时,如下图,圆N与OB相切时,NP2=MN=4,且NP2⊥OB,此时MP3=4,
则OM=ON-MN= ![]() NP2-4=
NP2-4= ![]() .
.
③因为MN=4,所以当x>0时,MN<ON,则MN=NP不存在,
除了P1外,当MP=MN=4时,
过点M作MD⊥OB于D,当OM=MP=4时,圆M与OB刚好交OB两点P2和P3;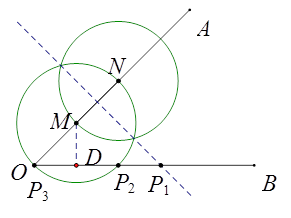
当MD=MN=4时,圆M与OB只有一个交点,此时OM= ![]() MD=4
MD=4 ![]() ,
,
故4≤x<4 ![]() .
.
与OB有两个交点P2和P3 ,
所以答案是x=0或x= ![]() 或4≤x<4
或4≤x<4 ![]() .
.
【考点精析】掌握相交两圆的性质是解答本题的根本,需要知道相交的两个圆的连心线垂直平分两圆的公共弦.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:初中数学 来源: 题型:
【题目】正方形A1B1C1O,A2B2C2C1 , A3B3C3C2 , …按如图所示的方式放置.点A1 , A2 , A3 , …和点C1 , C2 , C3 , …分别在直线y=kx+b(k>0)和x轴上,已知点B1(1,1),B2(3,2),则Bn的坐标是 . 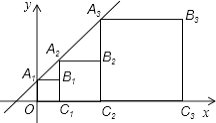
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠A+∠D=180°,∠1=3∠2,∠2=24°,点P是BC上的一点.
(1)请写出图中∠1的一对同位角,一对内错角,一对同旁内角;
(2)求∠EFC与∠E的度数;
(3)若∠BFP=46°,请判断CE与PF是否平行?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标xOy中,正比例函数y=﹣4x的图象经过点A(﹣3,m),点B在x轴的负半轴上,过点A作直线AC∥x轴,交∠AOB的平分线OC于点C,那么点C到直线OA的距离等于_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,要得到△ABD≌△ACE,从下列条件中补选一个,则错误的是( )

A.AB=AC B.DB=EC C.∠ADB=∠AEC D.∠B=∠C
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.从下列四个条件:①BC=B′C,②AC=A′C,③∠A′CA=∠B′CB,④AB=A′B′中,任取三个为条件,余下的一个为结论,则最多可以构成正确的结论的个数是( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB与CD交于点O,OE平分∠AOC,点F为AB上一点(不与点A及O重合),过点F作FG∥OE,交CD于点G,若∠AOD=110°,则∠AFG度数为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,对角线BD平分∠ABC,过点A作AE∥BD,交CD的延长线于点E,过点E作EF⊥BC,交BC延长线于点F. 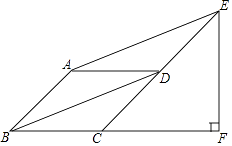
(1)求证:四边形ABCD是菱形;
(2)若∠ABC=45°,BC=2,求EF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com