
【题目】已知在平面直角坐标xOy中,正比例函数y=﹣4x的图象经过点A(﹣3,m),点B在x轴的负半轴上,过点A作直线AC∥x轴,交∠AOB的平分线OC于点C,那么点C到直线OA的距离等于_____.
 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:
【题目】点A在数轴上对应的数为![]() 点B对应的数为
点B对应的数为![]() 且
且![]() 满足
满足![]()
(1)线段AB的长为________;
(2)点C在数轴上对应的数为10,在数轴上是否存在点D,使得DA+DB=DC?若存在,求出点D对应的数;若不存在,说明理由。
(3)动点P从点A出发,以每秒6个单位长度的速度沿数轴向左均速运动;动点Q从点B出发,以每秒4个单位长度的速度沿数轴向左移动;动点M从点A出发,以每秒3个单位长度的速度沿数轴向左均速移动,点P、Q、M同时出发,设运动时间为![]() 秒,当
秒,当![]() 时,探究QP、QA、QM三条线段之间的数量关系,并说明理由.
时,探究QP、QA、QM三条线段之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学在商场购买甲、乙两种不同的运动器材,购买甲种器材花费1 500元,购买乙种器材花费1 000元,购买甲种器材数量是购买乙种器材数量的2倍,且购买一件乙种器材比购买一件甲种器材多花10元.
(1)求购买一件甲种器材、一件乙种器材各需多少元?
(2)该中学决定再次购买甲、乙两种运动器材共50件,恰逢该商场对两种运动器材的售价进行调整,甲种器材售价比第一次购买时提高了10%,乙种器材售价比第一次购买时降低了10%,如果此次购买甲、乙两种器材的总费用不超过1 700元,那么这所学校最多可购买多少件乙种器材?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明
如图,点E在直线DF上,点B在直线AC上,若∠AGB=∠EHF,∠C=∠D.
求证:∠A=∠F.

证明:∵∠AGB=∠EHF
∠AGB=___________(对顶角相等)
∴∠EHF=∠DGF
∴DB∥EC(____________________________________)
∴∠_________=∠DBA(________________________________)
又∵∠C=∠D
∴∠DBA=∠D
∴DF∥_______(__________________________________)
∴∠A=∠F(__________________________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOD=150°,OB、OC、OM、ON 是∠AOD 内的射线,若∠BOC=20°,∠AOB=10°,OM 平分∠AOC,ON 平分∠BOD,当∠BOC 在∠AOD 内绕着点 O以 3°/秒的速度逆时针旋转 t 秒时,当∠AOM:∠DON=3:4 时,则 t=____________.
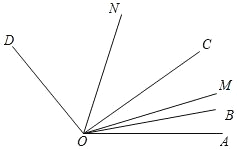
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=45°,点M,N在边OA上,OM=x,ON=x+4,点P是边OB上的点.若使点P,M,N构成等腰三角形的点P恰好有三个,则x的值是.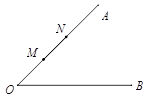
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育文化用品商店购进篮球和排球共30个,进价和售价如下表,若全部销售完后共可获利润1680元.
篮球 | 排球 | |
进价(元/个) | 150 | 120 |
售价(元/个) | 200 | 180 |
(1)请利用二元一次方程组求购进篮球和排球各多少个?
(2)“双11”快到了,这个体育文化用品商店也准备搞促销活动,计划篮球9折销售,排球8折销售,则销售8个篮球的利润与销售几个排球的利润相等?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com