
【题目】如图,Rt△ABC的两个锐角顶点A,B在函数y= ![]() (x>0)的图象上,AC//x轴,AC=2.若点A的坐标为(2,2),则点B的坐标为.
(x>0)的图象上,AC//x轴,AC=2.若点A的坐标为(2,2),则点B的坐标为.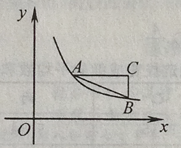
【答案】(4,1)
【解析】解:因为点A(2,2)在函数y= ![]() (x>0)的图象上,
(x>0)的图象上,
所以k=2×2=4.
则反比函数y= ![]() (x>0),
(x>0),
因为AC//x轴,AC=2,
所以C(4,2).
在Rt△ABC中,∠ACB=90°,
所以B的横坐标与C的横坐标相同,为4,
当x=4时,y= ![]() =1,
=1,
则B(4,1).
所以答案是(4,1).
【考点精析】利用反比例函数的图象和反比例函数的性质对题目进行判断即可得到答案,需要熟知反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点;性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大.


科目:初中数学 来源: 题型:
【题目】为加强中小学生安全和禁毒教育,某校组织了“防溺水、交通安全、禁毒”知识竞赛,为奖励在竞赛中表现优异的班级,学校准备从体育用品商场一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),购买1个足球和1个篮球共需159元;足球单价是篮球单价的2倍少9元.
(1)求足球和篮球的单价各是多少元?
(2)根据学校实际情况,需一次性购买足球和篮球共20个,但要求购买足球和篮球的总费用不超过1550元,学校最多可以购买多少个足球?
查看答案和解析>>
科目:初中数学 来源: 题型:
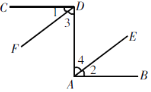
【题目】如图,已知CD⊥DA,DA⊥AB,∠1=∠2. 试说明DF∥AE. 请你完成下列填空,把解答过程补充完整.
解:∵CD⊥DA,DA⊥AB,
∴∠CDA=90°,∠DAB=90°( ).
∴∠CDA=∠DAB(等量代换).
又∠1=∠2,
从而∠CDA-∠1=∠DAB-________(等式的性质).
即∠3=_______.
∴DF∥AE( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答题
定义:把四边形的某些边向两方延长,其他各边有不在延长所得直线的同一旁,这样的四边形叫做凹四边形.如图1,四边形ABCD为凹四边形.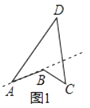
(1)性质探究:请完成凹四边形一个性质的证明.
已知:如图2,四边形ABCD是凹四边形.
求证:∠BCD=∠B+∠A+∠D.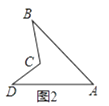
(2)性质应用:
如图3,在凹四边形ABCD中,∠BAD的角平分线与∠BCD的角平分线交于点E,若∠ADC=140°,∠AEC=102°,则∠B=°.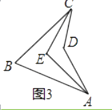
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标xOy中,正比例函数y=﹣4x的图象经过点A(﹣3,m),点B在x轴的负半轴上,过点A作直线AC∥x轴,交∠AOB的平分线OC于点C,那么点C到直线OA的距离等于_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:在△ABC中,∠ACB=90°,CD为高,且CD、CE三等分∠ACB.
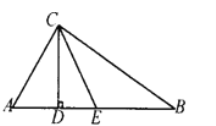
(1)求∠B的度数.
(2)求证:CE是AB边上的中线,且![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.从下列四个条件:①BC=B′C,②AC=A′C,③∠A′CA=∠B′CB,④AB=A′B′中,任取三个为条件,余下的一个为结论,则最多可以构成正确的结论的个数是( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
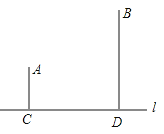
【题目】如图,牧童在A处放牛,其家在B处,A、B到河岸l的距离分别为AC=1km,BD=3km,且CD=3km.
(1)牧童从A处将牛牵到河边饮水后再回家,试问在何处饮水,所走路程最短?请用尺规在图中画出饮水的位置(保留作图痕迹,不写作法),并说明理由.
(2)求出(1)中的最短路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个三位数,若十位上的数字是百位数字与个位数字的和,我们称这个三位数叫“圣诞数”,并且把这个“圣诞数”的前两位组成的两位数记为m,后两位组成的两位数记为n,并规定d=![]() 。如一个三位数385,
。如一个三位数385,![]() 3+5=8,
3+5=8,![]() 385是“圣诞数”,且m=38,n=85,则d=
385是“圣诞数”,且m=38,n=85,则d=![]() =
=![]() .
.
(1)写出最小的“圣诞数”;
(2)求证:任意一个“圣诞数”是11的倍数;
(3)求出所有能被8整除的“圣诞数”,并直接写出这些“圣诞数”中d的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com