
【题目】完成下列推理过程:
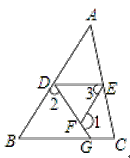
已知:如图,∠1+∠2=180°,∠3=∠B
求证:∠EDG+∠DGC=180°
证明:∵∠1+∠2=180°(已知)
∠1+∠DFE=180°( )
∴∠2= ( )
∴EF∥AB( )
∴∠3= ( )
又∵∠3=∠B(已知)
∴∠B=∠ADE( )
∴DE∥BC( )
∴∠EDG+∠DGC=180°( )
【答案】邻补角定义;∠DFE,同角的补角相等;内错角相等,两直线平行;∠ADE,两直线平行,内错角相等;等量代换;同位角相等,两直线平行;两直线平行,同旁内角互补
【解析】
依据∠1+∠2=180°,∠1+∠DFE=180°,即可得到∠2=∠DFE,由内错角相等,两直线平行证明EF∥AB,则∠3=∠ADE,再根据∠3=∠B,由同位角相等,两直线平行证明DE∥BC,故可根据两直线平行,同旁内角互补,即可得出结论.
∵∠1+∠2=180°(已知)
∠1+∠DFE=180°(邻补角定义)
∴∠2=∠DFE(同角的补角相等)
∴EF∥AB(内错角相等,两直线平行)
∴∠3=∠ADE(两直线平行,内错角相等)
又∵∠3=∠B(已知)
∴∠B=∠ADE(等量代换)
∴DE∥BC(同位角相等,两直线平行)
∴∠EDG+∠DGC=180°(两直线平行,同旁内角互补)


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,要得到△ABD≌△ACE,从下列条件中补选一个,则错误的是( )

A.AB=AC B.DB=EC C.∠ADB=∠AEC D.∠B=∠C
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店以40元/千克的进价购进一批茶叶,经调查发现,在一段时间内,销售量y(千克)与销售价x(元/千克)成一次函数关系,其图象如图所示.
(1)求y与x之间的函数关系式(不必写出自变量x的取值范围);
(2)若该商店销售这批茶叶的成本不超过2800元,则它的最低销售价应定为多少元? 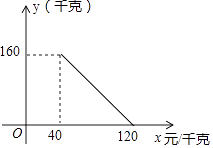
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程数.“燃油效率”越高表示汽车每消耗1升汽油行驶的里程数越多;“燃油效率”越低表示汽车每消耗1升汽油行驶的里程数越少.如图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况,下列说法中,正确的是( ) 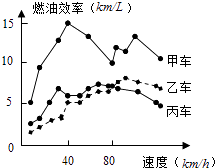
A.以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
B.以低于80km/h的速度行驶时,行驶相同路程,三辆车中,乙车消耗汽油最少
C.以高于80km/h的速度行驶时,行驶相同路程,丙车比乙车省油
D.以80km/h的速度行驶时,行驶100公里,甲车消耗的汽油量约为10升
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,D为BC边的中点,BE平分∠ABC,交AD于E,F为△ABC外一点,且∠ACF=![]() ∠ACB,BE=CF,
∠ACB,BE=CF,
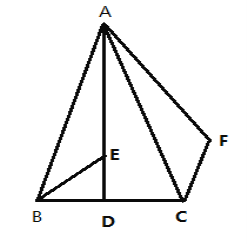
(1)求证:∠BAF=3∠BAD
(2)若DE=5,AE=13,求线段AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,对角线BD平分∠ABC,过点A作AE∥BD,交CD的延长线于点E,过点E作EF⊥BC,交BC延长线于点F. 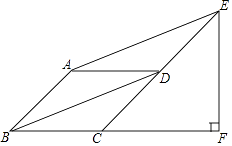
(1)求证:四边形ABCD是菱形;
(2)若∠ABC=45°,BC=2,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】湘西自治州风景优美,物产丰富,一外地游客到某特产专营店,准备购买精加工的豆腐乳和猕猴桃果汁两种盒装特产.若购买3盒豆腐乳和2盒猕猴桃果汁共需180元;购买1盒豆腐乳和3盒猕猴桃果汁共需165元.
(1)请分别求出每盒豆腐乳和每盒猕猴桃果汁的价格;
(2)该游客购买了4盒豆腐乳和2盒猕猴桃果汁,共需多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.
(1)试判断直线AB与直线CD的位置关系,并说明理由;
(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;
(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,问∠HPQ的大小是否发生变化?若不变,请求出其值;若变化,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于数轴上的A,B,C三点,给出如下定义:若其中一个点与其它两个点的距离恰好满足2倍的数量关系,则称该点是其它两个点的“联盟点”.
例如数轴上点A,B,C所表示的数分别为1,3,4,此时点B是点A, C的“联盟点”.
![]()
(1)若点A表示数-2, 点B表示的数2,下列各数![]() ,0,4,6所对应的点分别C1,C2 ,C3 ,C4,其中是点A,B的“联盟点”的是 ;
,0,4,6所对应的点分别C1,C2 ,C3 ,C4,其中是点A,B的“联盟点”的是 ;
(2)点A表示数-10, 点B表示的数30,P在为数轴上一个动点:
①若点P在点B的左侧,且点P是点A, B的“联盟点”,求此时点P表示的数;
②若点P在点B的右侧,点P,A, B中,有一个点恰好是其它两个点的“联盟点”,写出此时点P表示的数 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com