
【题目】对于数轴上的A,B,C三点,给出如下定义:若其中一个点与其它两个点的距离恰好满足2倍的数量关系,则称该点是其它两个点的“联盟点”.
例如数轴上点A,B,C所表示的数分别为1,3,4,此时点B是点A, C的“联盟点”.
![]()
(1)若点A表示数-2, 点B表示的数2,下列各数![]() ,0,4,6所对应的点分别C1,C2 ,C3 ,C4,其中是点A,B的“联盟点”的是 ;
,0,4,6所对应的点分别C1,C2 ,C3 ,C4,其中是点A,B的“联盟点”的是 ;
(2)点A表示数-10, 点B表示的数30,P在为数轴上一个动点:
①若点P在点B的左侧,且点P是点A, B的“联盟点”,求此时点P表示的数;
②若点P在点B的右侧,点P,A, B中,有一个点恰好是其它两个点的“联盟点”,写出此时点P表示的数 .
【答案】(1)![]() ,
,![]() ;(2)①-50或
;(2)①-50或![]() 或
或![]() ;②50或70或110.
;②50或70或110.
【解析】
(1)题目给定的规律,联盟点必须满足其中一个点与其它两个点的距离恰好满足2倍的数量关系,根据规律找出即可(2)已知点A的大小,点B的大小,根据不同的位置分别找出点P的坐标即可.
解:(1)![]() ,
,![]() ;
;
(2)① 设点P表示的数为x,
![]()
如图,当点![]() 在点A左侧时,
在点A左侧时,![]() ,
,
则 30-x=2(-10-x),
解得 x=-50.
所以点![]() 表示的数为-50;
表示的数为-50;
如图,当点![]() 在线段AB上且
在线段AB上且![]() 时,
时,
![]()
则 30-x=2(x+10),
解得 x=![]() .
.
所以点![]() 表示的数为
表示的数为![]() ;
;
如图,当点![]() 在线段AB上且
在线段AB上且![]() 时,
时,
![]()
则 x+10=2(30-x),
解得 x=![]() .
.
所以点![]() 表示的数为
表示的数为![]() .
.
综上所述,当点P在点B的左侧时,点P表示的数为-50或![]() 或
或![]() .
.
② 50或70或110.


科目:初中数学 来源: 题型:
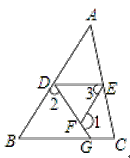
【题目】完成下列推理过程:
已知:如图,∠1+∠2=180°,∠3=∠B
求证:∠EDG+∠DGC=180°
证明:∵∠1+∠2=180°(已知)
∠1+∠DFE=180°( )
∴∠2= ( )
∴EF∥AB( )
∴∠3= ( )
又∵∠3=∠B(已知)
∴∠B=∠ADE( )
∴DE∥BC( )
∴∠EDG+∠DGC=180°( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+8(a≠0)与x轴交于A(﹣2,0),B两点,与y轴交于C点,tan∠ABC=2. 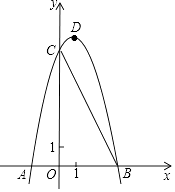
(1)求抛物线的表达式及其顶点D的坐标;
(2)过点A、B作x轴的垂线,交直线CD于点E、F,将抛物线沿其对称轴向上平移m个单位,使抛物线与线段EF(含线段端点)只有1个公共点.求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义一种对正整数n的“C运算”:①当n为奇数时,结果为3n+1;②当n为偶数时,结果为![]() (其中k是使
(其中k是使![]() 为奇数的正整数),并且运算重复进行.例如,n=66时,其“C运算”如下
为奇数的正整数),并且运算重复进行.例如,n=66时,其“C运算”如下
![]()
若n=26,则第2019次“C运算”的结果是
A. 40 B. 5 C. 4 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知直线l1:y=mx(m≠0)与直线l2:y=ax+b(a≠0)相交于点A(1,2),直线l2与x轴交于点B(3,0).
(1)分别求直线l1和l2的表达式;
(2)过动点P(0,n)且平行于x轴的直线与l1 , l2的交点分别为C,D,当点C位于点D左方时,写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=1,BC=2,则△ABE和△BC′F的周长之和为( ) 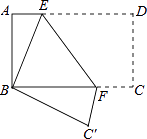
A.3
B.4
C.6
D.8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com