
【题目】四边形ABCD中,∠A=∠C=90°,BE、DF分别是∠ABC、∠ADC的平分线.求证:
(1)、∠1+∠2=90°;(2)、BE∥DF.

【答案】(1)、证明过程见解析;(2)、证明过程见解析
【解析】
试题分析:(1)、根据角平分线的性质得出∠1=∠ABE,∠2=∠ADF。根据四边形内角和定理可得∠ABC+∠ADC=180°,即2(∠1+∠2)=180°,从而得出答案;(2)、根据三角形内角和定理可得∠DFC+∠2=90°,结合第一题的结论得出∠1=∠DFC,从而得出答案.
试题解析:(1)、∵BE,DF分别是∠ABC,∠ADC的平分线, ∴∠1=∠ABE,∠2=∠ADF,
∵∠A=∠C=90°, ∴∠ABC+∠ADC=180°, ∴2(∠1+∠2)=180°, ∴∠1+∠2=90°;
(2)、在△FCD中,∵∠C=90°, ∴∠DFC+∠2=90°, ∵∠1+∠2=90°,
∴∠1=∠DFC, ∴BE∥DF.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:
【题目】直角△ABC中,∠C=90°,点D,E分别是边AC,BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.
(1)若点P在线段AB上,如图①,且∠α=50°,则∠1+∠2= ;
(2)若点P在斜边AB上运动,如图②,则∠α、∠1、∠2之间的关系为 ;
(3)如图③,若点P在斜边BA的延长线上运动(CE<CD),请直接写出∠α、∠1、∠2之间的关系: ;
(4)若点P运动到△ABC形外(只需研究图④情形),则∠α、∠1、∠2之间有何关系?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的三个顶点分别为A(2,3)、B(3,1)、C(﹣2,﹣2).

(1)请在图中作出△ABC关于直线x=﹣1的轴对称图形△DEF(A、B、C的对应点分别是D、E、F),并直接写出D、E、F的坐标;
(2)求四边形ABED的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料
小明遇到这样一个问题:求计算![]() 所得多项式的一次项系数.
所得多项式的一次项系数.
小明想通过计算![]() 所得的多项式解决上面的问题,但感觉有些繁琐,他想探寻一下,是否有相对简洁的方法.
所得的多项式解决上面的问题,但感觉有些繁琐,他想探寻一下,是否有相对简洁的方法.
他决定从简单情况开始,先找![]() 所得多项式中的一次项系数.通过观察发现:
所得多项式中的一次项系数.通过观察发现:

也就是说,只需用![]() 中的一次项系数1乘以
中的一次项系数1乘以![]() 中的常数项3,再用
中的常数项3,再用![]() 中的常数项2乘以
中的常数项2乘以![]() 中的一次项系数2,两个积相加
中的一次项系数2,两个积相加![]() ,即可得到一次项系数.
,即可得到一次项系数.
延续上面的方法,求计算![]() 所得多项式的一次项系数.可以先用
所得多项式的一次项系数.可以先用![]() 的一次项系数1,
的一次项系数1, ![]() 的常数项3,
的常数项3, ![]() 的常数项4,相乘得到12;再用
的常数项4,相乘得到12;再用![]() 的一次项系数2,
的一次项系数2, ![]() 的常数项2,
的常数项2, ![]() 的常数项4,相乘得到16;然后用
的常数项4,相乘得到16;然后用![]() 的一次项系数3,
的一次项系数3, ![]() 的常数项2,
的常数项2, ![]() 的常数项3,相乘得到18.最后将12,16,18相加,得到的一次项系数为46.
的常数项3,相乘得到18.最后将12,16,18相加,得到的一次项系数为46.
参考小明思考问题的方法,解决下列问题:
(1)计算![]() 所得多项式的一次项系数为 .
所得多项式的一次项系数为 .
(2)计算![]() 所得多项式的一次项系数为 .
所得多项式的一次项系数为 .
(3)若计算![]() 所得多项式的一次项系数为0,则
所得多项式的一次项系数为0,则![]() =_________.
=_________.
(4)若![]() 是
是![]() 的一个因式,则
的一个因式,则![]() 的值为 .
的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题:如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣1,4),C(﹣3,2).
(1)画出△ABC关于y轴对称的图形△A1B1C1,并直接写出C1点坐标;
(2)以原点O为位似中心,位似比为1:2,在y轴的左侧,画出△ABC放大后的图形△A2B2C2,并直接写出C2点坐标;
(3)如果点D(a,b)在线段AB上,请直接写出经过(2)的变化后D的对应点D2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成,硬纸板如图两种方法裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面; B方法:剪4个侧面和5个底面。
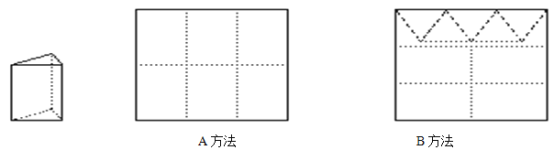
现有38张硬纸板,裁剪时x张用A方法,其余用B方法。
(1)用x的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“春种一粒栗,秋收万颗子”,唐代诗人李绅这句诗中的“粟”即谷子(去皮后则称为“小米”),被誉为中华民族的哺育作物。我省有着“小杂粮王国”的美誉,谷子作为我省杂粮谷物中的大类,其种植面积已连续多年全国第一.2016年全国谷子的种植面积为2000万亩,年总产量为150万吨,我省谷子平均亩产量为160kg,国内其他地区谷子的平均亩产量为60kg.请解答下列问题:
(1)求我省2016年谷子的种植面积是多少万亩;
(2)2017年,若我省谷子的平均亩产量仍保持160kg不变,要使我省谷子的年总产量达到52万吨,那么今年我省应再多种植多少万亩的谷子?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的弦,点C是在过点B的切线上,且OC⊥OA,OC交AB于点P.
(1)判断△CBP的形状,并说明理由;
(2)若⊙O的半径为6,AP=![]() ,求BC的长.
,求BC的长.
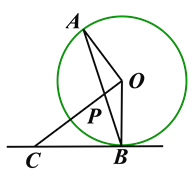
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,BD为△ABC的的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足.下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=AE=EC;④BA+BC=2BF.其中正确的是( )
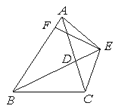
A.①②③ B.①③④ C.①②④ D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com