
【题目】解方程:
(1)![]() =2﹣
=2﹣![]()
(2)![]() ﹣
﹣![]() =﹣1
=﹣1
【答案】(1)y=3;(2)x=﹣![]() .
.
【解析】
方程两边每一项都要乘各分母的最小公倍数10,切勿漏乘不含有分母的项,另外分数线有两层意义,一方面它是除号,另一方面它又代表着括号,所以在去分母时,应该将分子用括号括上.
方程左边分子分母同时扩大10倍,两边每一项都要乘各分母的最小公倍数6,切勿漏乘不含有分母的项,另外分数线有两层意义,一方面它是除号,另一方面它又代表着括号,所以在去分母时,应该将分子用括号括上.
(1)去分母,得5(y﹣1)=20-2(y+2),
去括号,得5y-5=20-2y-4,
移项,得5y+2y=20-4+5,
整理,得7y=21,
解得,y=3.
(2)方程可变形为![]()
去分母,得2(10x-30)-3(20x+1)=-6,
去括号,得20x-60-60x-3=-6,
移项并整理,得-40x=57
解得,x=﹣![]() .
.


科目:初中数学 来源: 题型:
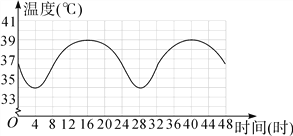
【题目】某生物兴趣小组在四天的实验研究中发现:骆驼的体温会随外部环境温度的变化而变化,而且在这四天中每昼夜的体温变化情况相同.他们将一头骆驼前两昼夜的体温变化情况绘制成下图.请根据图像回答问题:
(1)第一天中,在什么时间范围内这头骆驼的体温是上升的?它的体温从最低上升到最高需要多少时间?
(2)第三天12时这头骆驼的体温约是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
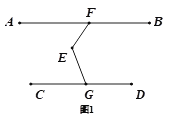
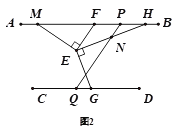
【题目】已知:F、G分别为直线AB、CD上的点,E为平面内任意一点,连接EF、EG,∠AFE+∠CGE=∠FEG.
(1)如图(1),求证:AB∥CD,
(2)如图(2),过点E作EM⊥EF、EH⊥EG交直线AB上的点M、H,点N在EH上,过N作PQ∥EF.求证∶∠HNQ=∠MEG.
(3)如图(3)在(2)的条件下,若∠ENQ=∠EMF,∠EGD=110°,求∠CQP的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BE是它的角平分线,∠C=90°,D在AB边上,以DB为直径的半圆O经过点E,交BC于点F. 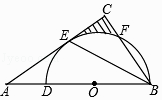
(1)求证:AC是⊙O的切线;
(2)已知cosA= ![]() ,⊙O的半径为3,求图中阴影部分的面积.
,⊙O的半径为3,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=4,则四边形OCED的周长为( ) 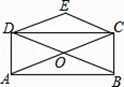
A.4
B.8
C.10
D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像交于第一、三象限内的
的图像交于第一、三象限内的![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 在
在![]() 轴负半轴上,
轴负半轴上,![]() ,且四边形
,且四边形![]() 是平行四边形,点
是平行四边形,点![]() 的纵坐标为
的纵坐标为![]() .
.
(1)求该反比例函数和一次函数的表达式;
(2)连接![]() ,求
,求![]() 的面积;
的面积;
(3)直接写出关于![]() 的不等式
的不等式![]() 的解集.
的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列结论:①若![]() 是关于x的方程a
是关于x的方程a![]() 的一个解,则
的一个解,则![]() ;②若
;②若![]() ,则关于x的方程
,则关于x的方程![]() 有唯一的解;③若
有唯一的解;③若![]() ,则关于x的方程
,则关于x的方程![]() (
(![]() )的解为
)的解为![]() ;④若
;④若![]() ,且
,且![]() ,则
,则![]() 一定是方程
一定是方程![]() 的解.其中,结论正确的有( )
的解.其中,结论正确的有( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线AC、BD的长分别是6cm、8cm,AE⊥BC于点E,则AE的长是( ) 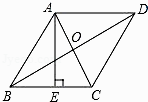
A.![]() cm
cm
B.![]() cm
cm
C.![]() cm
cm
D.5 ![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,六边形ABCDEF的内角都相等,∠DAB=60°,AB=DE,则下列结论成立的个数是( )
①AB∥DE;②EF∥AD∥BC;③AF=CD;④四边形ACDF是平行四边形;⑤六边形ABCDEF既是中心对称图形,又是轴对称图形.
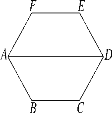
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com