
【题目】已知:F、G分别为直线AB、CD上的点,E为平面内任意一点,连接EF、EG,∠AFE+∠CGE=∠FEG.
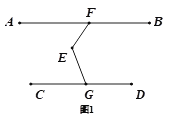
(1)如图(1),求证:AB∥CD,
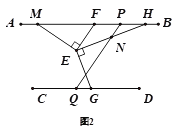
(2)如图(2),过点E作EM⊥EF、EH⊥EG交直线AB上的点M、H,点N在EH上,过N作PQ∥EF.求证∶∠HNQ=∠MEG.
(3)如图(3)在(2)的条件下,若∠ENQ=∠EMF,∠EGD=110°,求∠CQP的度数.

【答案】(1)证明见解析;(2)证明见解析;(3)125°.
【解析】
(1)过E作ET∥AB,证得∠GET=∠EGC,从而ET∥CD,因此可得结论;
(2)根据EM⊥EF、EH⊥EG,得∠MEG+∠FEN=180°;根据PQ∥EF得∠PNE+∠FEN=180°,∠HNQ=∠PNE,故∠HNQ=∠MEG;
(3)设∠FME=α 则α+α+20°=90°,求得α=35°, 因此∠MPN=∠MFE=55°,故∠PQC=125°.
(1)过E作ET∥AB.
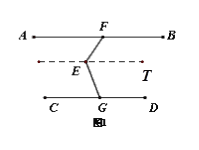
则∠AFE=∠FET,
∵∠FET+∠GET=∠FEG,
∠AFE+∠CGE=∠FEG,
∴∠GET=∠EGC,
∴ET∥CD,
∴AB∥CD;
(2)如图,
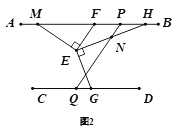
∵EM⊥EF、EH⊥EG,
∴∠MEG+∠FEN=180°,
∵PQ∥EF
∴∠PNE+∠FEN=180°,∠HNQ=∠PNE
∴∠HNQ=∠MEG
(3)过E作ET∥AB,
设∠FME=α ,
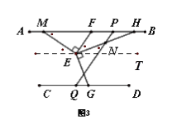
∵α+α+20°=90°,
∴α=35°,
∴∠MPN=∠MFE=α+20°=55°,
∴∠PQC=180°-55°=125°.


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:
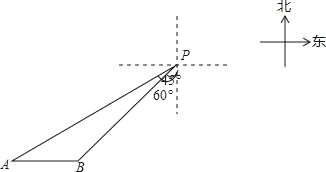
【题目】一艘轮船位于灯塔P南偏西60°方向的A处,它向东航行20海里到达灯塔P南偏西45°方向上的B处,若轮船继续沿正东方向航行,求轮船航行途中与灯塔P的最短距离.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AB=AC,点D在BC上,且BD=BA,点E在BC的延长线上,且CE=CA.
(1)试求∠DAE的度数;
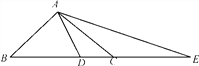
(2)如果把原题中“AB=AC”的条件去掉,其余条件不变,那么∠DAE的度数会改变吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育用品商场采购员要到厂家批发购进篮球和排球共100只,付款总额不得超过11 815元.已知两种球厂家的批发价和商场的零售价如右表,试解答下列问题:
品名 | 厂家批发价(元/只) | 市场零售价(元/只) |
篮球 | 130 | 160 |
排球 | 100 | 120 |
(1)该采购员最多可购进篮球多少只?
(2)若该商场把这100只球全部以零售价售出,为使商场获得的利润不低于2580元,则采购员至少要购篮球多少只,该商场最多可盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,E,F是对角线BD上的两点,如果添加一个条件,使△ABE ≌ △CDF,则添加的条件不能为( )
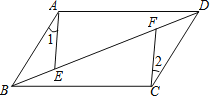
A. BE=DF B. BF=DE C. ∠1=∠2 D. AE=CF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线AB∥CD,直线l与直线AB、CD相交于点,E、F,将l绕点E逆时针旋转40°后,与直线AB相交于点G,若∠GEC=70°,那么∠GFE=度. 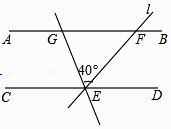
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按下面的程序计算:当输入x=100 时,输出结果是299;当输入x=50时,输出结果是446;如果输入 x 的值是正整数,输出结果是257,那么满足条件的x的值最多有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(2,y1)、B(4,y2)都在反比例函数![]() (k<0)的图象上,则y1、y2的大小关系为( )
(k<0)的图象上,则y1、y2的大小关系为( )
A. y1>y2 B. y1<y2 C. y1=y2 D. 无法确定
【答案】B
【解析】试题∵当k<0时,y=![]() 在每个象限内,y随x的增大而增大,∴y1<y2,故选B.
在每个象限内,y随x的增大而增大,∴y1<y2,故选B.
考点:反比例函数增减性.
【题型】单选题
【结束】
17
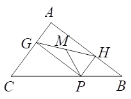
【题目】如图, 在△ABC中,AC=3、AB=4、BC=5, P为BC上一动点,PG⊥AC于点G,PH⊥AB
于点H,M是GH的中点,P在运动过程中PM的最小值为( )
A. 2.4 B. 1.4
C. 1.3 D. 1.2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com