
【题目】如图,已知直线AB∥CD,直线l与直线AB、CD相交于点,E、F,将l绕点E逆时针旋转40°后,与直线AB相交于点G,若∠GEC=70°,那么∠GFE=度. 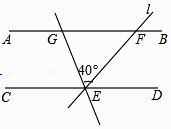
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】往一个长25m,宽11m的长方体游泳池注水,水位每小时上升0.32m,
(1)写出游泳池水深d(m)与注水时间x(h)的函数表达式;
(2)如果x(h)共注水y(m3),求y与x的函数表达式;
(3)如果水深1.6m时即可开放使用,那么需往游泳池注水几小时?注水多少(单位:m3)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学为了深入学习社会主义核心价值观,特对本校部分学生(随机抽样)进行了一次相关知识的测试(成绩分为A、B、C、D、E五个组,x表示测试成绩),A组:90≤x≤100 B组:80≤x<90 C组:70≤x<80 D组:60≤x<70 E组:x<60;通过对测试成绩的分析,得到如图所示的两幅不完整的统计图,请你根据图中提供的信息解答以下问题. 
(1)填空:参加调查测试的学生共有人;A组所占的百分比为 , 在扇形统计图中,C组所在扇形的圆心角为度;
(2)请将条形统计图补充完整.
(3)本次调查测试成绩在80分以上(含80分)为优秀,该中学共有3000人,请估计全校测试成绩为优秀的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB∥CD,∠BCD=90°,AB=AD=10cm,BC=8cm,点P从点A出发,以每秒2cm的速度沿线段AB向点B方向运动,点Q从点D出发,以每秒3cm的速度沿线段DC向点C运动,已知动点P、Q同时出发,点P到达B点或点Q到达C点时,P、Q运动停止,设运动时间为t (秒).
(1)求CD的长;
(2)当四边形PBQD为平行四边形时,求t的值;
(3)在点P、点Q的运动过程中,是否存在某一时刻,使得PQ⊥AB?若存在,请求出t的值并说明理由;若不存在,请说明理
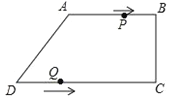

查看答案和解析>>
科目:初中数学 来源: 题型:
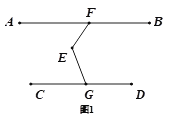
【题目】已知:F、G分别为直线AB、CD上的点,E为平面内任意一点,连接EF、EG,∠AFE+∠CGE=∠FEG.
(1)如图(1),求证:AB∥CD,
(2)如图(2),过点E作EM⊥EF、EH⊥EG交直线AB上的点M、H,点N在EH上,过N作PQ∥EF.求证∶∠HNQ=∠MEG.
(3)如图(3)在(2)的条件下,若∠ENQ=∠EMF,∠EGD=110°,求∠CQP的度数.
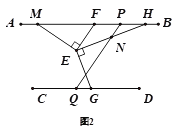

查看答案和解析>>
科目:初中数学 来源: 题型:
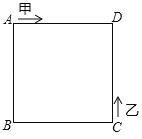
【题目】如图,甲、乙两动点分别从正方形ABCD的顶点A.C同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行.若甲的速度是乙的速度的3倍,则它们第2015次相遇在边________上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BE是它的角平分线,∠C=90°,D在AB边上,以DB为直径的半圆O经过点E,交BC于点F. 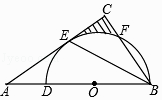
(1)求证:AC是⊙O的切线;
(2)已知cosA= ![]() ,⊙O的半径为3,求图中阴影部分的面积.
,⊙O的半径为3,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像交于第一、三象限内的
的图像交于第一、三象限内的![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 在
在![]() 轴负半轴上,
轴负半轴上,![]() ,且四边形
,且四边形![]() 是平行四边形,点
是平行四边形,点![]() 的纵坐标为
的纵坐标为![]() .
.
(1)求该反比例函数和一次函数的表达式;
(2)连接![]() ,求
,求![]() 的面积;
的面积;
(3)直接写出关于![]() 的不等式
的不等式![]() 的解集.
的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)![]() (2)
(2)![]()
(3)![]()
【答案】(1) ![]() ;(2)
;(2) ![]() ;(3)
;(3) ![]() .
.
【解析】(1)先化成最简二次根式,再合并同类二次根式即可;
(2)先算乘法和除法,再合并同类项或同类二次根式即可;
(3)第一项根据平方差公式计算,第二项根据完全平方公式计算,然后合并同类项或同类二次根式即可;
(1)原式=![]() =
= ![]()
(2)原式=![]() =
=![]()
(3)原式=![]() =
=![]()
点睛:本题考查了二次根式的性质与化简,二次根式的混合运算,熟练掌握二次根式的运算法则是解答本题的关键.
【题型】解答题
【结束】
19
【题目】(1)化简: ![]() (2)解方程:
(2)解方程:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com