
【题目】如图,在△ABC中,BE是它的角平分线,∠C=90°,D在AB边上,以DB为直径的半圆O经过点E,交BC于点F. 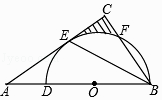
(1)求证:AC是⊙O的切线;
(2)已知cosA= ![]() ,⊙O的半径为3,求图中阴影部分的面积.
,⊙O的半径为3,求图中阴影部分的面积.
【答案】
(1)解:连接OE,
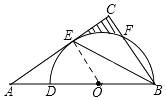
∴BE是∠OBC的角平分线,
∴∠OBE=∠CBE,
∵OE=OB,
∴∠OEB=∠OBE,
∴∠OEB=∠CBE,
∴OE∥BC,
∴∠AEO=∠C=90°,
∵OE是⊙O的半径,
∴AC是⊙O的切线;
(2)解:连接OF,
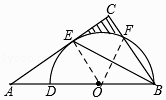
∵cosA= ![]() ,
,
∴∠A=30°,
∴∠ABC=∠AOE=60°
∵OB=OF=3,
∴∠FOB=∠ABC=60°,
∴∠EOF=60°,
∴扇形OEF的面积为: ![]() =
= ![]() ,
,
∵OE=3,∠BAC=30°,
∴AO=2OE=6,
∴AB=AO+OB=9,
∴BC= ![]() AB=
AB= ![]()
∴由勾股定理可知:AE=3 ![]() ,AC=
,AC= ![]() ,
,
∴CE=AC﹣AE= ![]() ,
,
∵BF=OB=3,
∴CF=BC﹣BF= ![]()
∴梯形OFCE的面积为: ![]() =
= ![]() ,
,
∴阴影部分面积为: ![]() ﹣
﹣ ![]()
【解析】(1)连接,根据BE平分∠OBC,OE=OB,可得出OE∥BC,从而可知∠AEO=∠C=90°,根据切线的判定,即可得出AC是⊙O的切线;(2)连接OF,根据条件分别求出OE、CF、CE,∠EOF的数值后,根据面积公式分别计算梯形OFCE与扇形EOF的面积,从而可求出阴影部分的面积.


科目:初中数学 来源: 题型:
【题目】一个不透明的布袋里装有16个只有颜色不同的球,其中红球有x个,白球有2x个,其他均为黄球,现甲从布袋中随机摸出一个球,若是红球则甲同学获胜,甲同学把摸出的球放回并搅匀,由乙同学随机摸出一个球,若为黄球,则乙同学获胜。
(1)当X=3时,谁获胜的可能性大?
(2)当x为何值时,游戏对双方是公平的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育用品商场采购员要到厂家批发购进篮球和排球共100只,付款总额不得超过11 815元.已知两种球厂家的批发价和商场的零售价如右表,试解答下列问题:
品名 | 厂家批发价(元/只) | 市场零售价(元/只) |
篮球 | 130 | 160 |
排球 | 100 | 120 |
(1)该采购员最多可购进篮球多少只?
(2)若该商场把这100只球全部以零售价售出,为使商场获得的利润不低于2580元,则采购员至少要购篮球多少只,该商场最多可盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线AB∥CD,直线l与直线AB、CD相交于点,E、F,将l绕点E逆时针旋转40°后,与直线AB相交于点G,若∠GEC=70°,那么∠GFE=度. 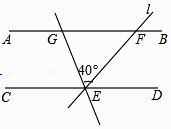
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按下面的程序计算:当输入x=100 时,输出结果是299;当输入x=50时,输出结果是446;如果输入 x 的值是正整数,输出结果是257,那么满足条件的x的值最多有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形![]() 中,对角线
中,对角线![]() 与
与![]() 相交于点
相交于点![]() .要使四边形
.要使四边形![]() 是正方形,还需添加一组条件.下面给出了五组条件:①
是正方形,还需添加一组条件.下面给出了五组条件:①![]() ,且
,且![]() ;②
;②![]() , 且
, 且![]() ;③
;③![]() ,且
,且![]() ;④
;④![]() ,且
,且![]() ;⑤
;⑤![]() ,且
,且![]() .其中正确的是________(填写序号).
.其中正确的是________(填写序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验室里,水平桌面上有甲、乙、丙三个相 同高度的圆柱形容器(容器足够高),底面半径之比为1:2:1,用两个相同的管子在10cm高度处连通(即管子底部离容器底10cm),现三个容器中,只有乙中有水,水位高4cm,如图所示.若每分钟同时向甲和丙注入相同量的水,开始注水1分钟,甲的水位上升3cm.则开始注入 分钟水量后,甲的水位比乙高1cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣x+b与反比例函数y= ![]() 的图象相交于A(1,4),B两点,延长AO交反比例函数图象于点C,连接OB.
的图象相交于A(1,4),B两点,延长AO交反比例函数图象于点C,连接OB. 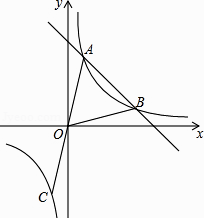
(1)求k和b的值;
(2)直接写出一次函数值小于反比例函数值的自变量x的取值范围;
(3)在y轴上是否存在一点P,使S△PAC= ![]() S△AOB?若存在请求出点P坐标,若不存在请说明理由.
S△AOB?若存在请求出点P坐标,若不存在请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com