
【题目】在平行四边形![]() 中,对角线
中,对角线![]() 与
与![]() 相交于点
相交于点![]() .要使四边形
.要使四边形![]() 是正方形,还需添加一组条件.下面给出了五组条件:①
是正方形,还需添加一组条件.下面给出了五组条件:①![]() ,且
,且![]() ;②
;②![]() , 且
, 且![]() ;③
;③![]() ,且
,且![]() ;④
;④![]() ,且
,且![]() ;⑤
;⑤![]() ,且
,且![]() .其中正确的是________(填写序号).
.其中正确的是________(填写序号).
【答案】①②③⑤
【解析】
由矩形、菱形、正方形的判定方法对各个选项进行判断即可.
∵四边形ABCD是平行四边形,AB=AD,∴四边形ABCD是菱形.
又∵AC=BD,∴四边形ABCD是矩形,∴平行四边形ABCD是正方形,①正确;
∵四边形ABCD是平行四边形,AB⊥AD,∴四边形ABCD是矩形.
又∵AC⊥BD,∴四边形ABCD是菱形,∴平行四边形ABCD是正方形,②正确;
∵四边形ABCD是平行四边形,AB=AD,∴四边形ABCD是菱形.
又∵AB⊥AD,∴四边形ABCD是正方形,③正确;
∵四边形ABCD是平行四边形,AB=BD,AB⊥BD,∴平行四边形ABCD不可能是正方形,④错误;
∵四边形ABCD是平行四边形,OB=OC,∴AC=BD,∴四边形ABCD是矩形,又OB⊥OC,即对角线互相垂直,∴平行四边形ABCD是正方形,⑤正确.
故答案为:①②③⑤.


科目:初中数学 来源: 题型:
【题目】已知一个有50个奇数排成的数阵,用如图所示的框去框住四个数,并求出这四个数的和,在下列给出的备选答案中,有可能是这四个数的和的是( )
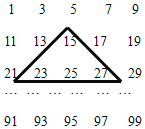
A. 114 B. 122 C. 220 D. 84
查看答案和解析>>
科目:初中数学 来源: 题型:
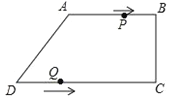
【题目】如图,在四边形ABCD中,AB∥CD,∠BCD=90°,AB=AD=10cm,BC=8cm,点P从点A出发,以每秒2cm的速度沿线段AB向点B方向运动,点Q从点D出发,以每秒3cm的速度沿线段DC向点C运动,已知动点P、Q同时出发,点P到达B点或点Q到达C点时,P、Q运动停止,设运动时间为t (秒).
(1)求CD的长;
(2)当四边形PBQD为平行四边形时,求t的值;
(3)在点P、点Q的运动过程中,是否存在某一时刻,使得PQ⊥AB?若存在,请求出t的值并说明理由;若不存在,请说明理

查看答案和解析>>
科目:初中数学 来源: 题型:
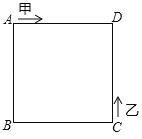
【题目】如图,甲、乙两动点分别从正方形ABCD的顶点A.C同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行.若甲的速度是乙的速度的3倍,则它们第2015次相遇在边________上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BE是它的角平分线,∠C=90°,D在AB边上,以DB为直径的半圆O经过点E,交BC于点F. 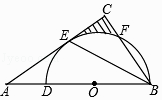
(1)求证:AC是⊙O的切线;
(2)已知cosA= ![]() ,⊙O的半径为3,求图中阴影部分的面积.
,⊙O的半径为3,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:五莲县新玛特购物中心第一次用5000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的![]() 倍多15件,甲、乙两种商品的进价和售价如下表(注:获利=售价﹣进价)
倍多15件,甲、乙两种商品的进价和售价如下表(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 20 | 30 |
售价(元/件) | 29 | 40 |
(1)新玛特购物中心将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(2)该购物中心第二次以第一次的进价又购进甲、乙两种商品,其中甲种商品的件数不变,乙种商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得总利润比第一次获得的总利润多160元,求第二次乙种商品是按原价打几折销售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像交于第一、三象限内的
的图像交于第一、三象限内的![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 在
在![]() 轴负半轴上,
轴负半轴上,![]() ,且四边形
,且四边形![]() 是平行四边形,点
是平行四边形,点![]() 的纵坐标为
的纵坐标为![]() .
.
(1)求该反比例函数和一次函数的表达式;
(2)连接![]() ,求
,求![]() 的面积;
的面积;
(3)直接写出关于![]() 的不等式
的不等式![]() 的解集.
的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两地相距64 km,甲从A地出发,每小时行14 km,乙从B地出发,每小时行18 km.
(1)若两人同时出发相向而行,则需经过几小时两人相遇?
(2)若两人同时出发相向而行,则需经过几小时两人相距16 km?
(3)若甲在前,乙在后,两人同时同向而行,则几小时后乙超过甲10 km?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作⊙O的切线,交OD的延长线于点E,连接BE. 
(1)求证:BE与⊙O相切;
(2)连接AD并延长交BE于点F,若OB=9,sin∠ABC= ![]() ,求BF的长.
,求BF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com