
【题目】已知:如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作⊙O的切线,交OD的延长线于点E,连接BE. 
(1)求证:BE与⊙O相切;
(2)连接AD并延长交BE于点F,若OB=9,sin∠ABC= ![]() ,求BF的长.
,求BF的长.
【答案】
(1)证明:连接OC,
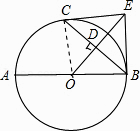
∵OD⊥BC,
∴∠COE=∠BOE,
在△OCE和△OBE中,
∵ 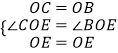 ,
,
∴△OCE≌△OBE,
∴∠OBE=∠OCE=90°,即OB⊥BE,
∵OB是⊙O半径,
∴BE与⊙O相切.
(2)解:过点D作DH⊥AB,连接AD并延长交BE于点F,
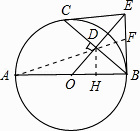
∵∠DOH=∠BOD,∠DHO=∠BDO=90°,
∴△ODH∽△OBD,
∴ ![]() =
= ![]() =
= ![]()
又∵sin∠ABC= ![]() ,OB=9,
,OB=9,
∴OD=6,
易得∠ABC=∠ODH,
∴sin∠ODH= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴OH=4,
∴DH= ![]() =2
=2 ![]() ,
,
又∵△ADH∽△AFB,
∴ ![]() =
= ![]() ,
, ![]() =
= ![]() ,
,
∴FB= ![]()
【解析】(1)连接OC,先证明△OCE≌△OBE,得出EB⊥OB,从而可证得结论.(2)过点D作DH⊥AB,根据sin∠ABC= ![]() ,可求出OD=6,OH=4,HB=5,然后由△ADH∽△AFB,利用相似三角形的性质得出比例式即可解出BF的长.
,可求出OD=6,OH=4,HB=5,然后由△ADH∽△AFB,利用相似三角形的性质得出比例式即可解出BF的长.


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
【题目】在平行四边形![]() 中,对角线
中,对角线![]() 与
与![]() 相交于点
相交于点![]() .要使四边形
.要使四边形![]() 是正方形,还需添加一组条件.下面给出了五组条件:①
是正方形,还需添加一组条件.下面给出了五组条件:①![]() ,且
,且![]() ;②
;②![]() , 且
, 且![]() ;③
;③![]() ,且
,且![]() ;④
;④![]() ,且
,且![]() ;⑤
;⑤![]() ,且
,且![]() .其中正确的是________(填写序号).
.其中正确的是________(填写序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的面积为12,△ABC是等边三角形,点E在正方形ABCD内,对角线AC上有一点P使PE+PD的和最小,这个最小值为( )

A. ![]() B.
B. ![]() C. 3 D.
C. 3 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
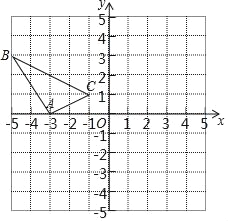
【题目】在边长为1个单位长度的小正方形组成的网格中,建立如图所示的平面直角坐标系△ABC是格点三角形(顶点在网格线的交点上)
(1)先作△ABC关于原点O成中心对称的△A1B1C1,再把△A1B1C1向上平移4个单位长度得到△A2B2C2;
(2)△A2B2C2与△ABC是否关于某点成中心对称?若是,直接写出对称中心的坐标;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣x+b与反比例函数y= ![]() 的图象相交于A(1,4),B两点,延长AO交反比例函数图象于点C,连接OB.
的图象相交于A(1,4),B两点,延长AO交反比例函数图象于点C,连接OB. 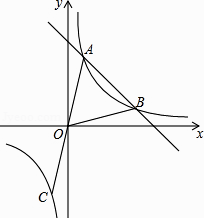
(1)求k和b的值;
(2)直接写出一次函数值小于反比例函数值的自变量x的取值范围;
(3)在y轴上是否存在一点P,使S△PAC= ![]() S△AOB?若存在请求出点P坐标,若不存在请说明理由.
S△AOB?若存在请求出点P坐标,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,长方形OABC的边OA在数轴上,O为原点,长方形OABC的面积为12,OC边长为3.

(1)数轴上点A表示的数为________.
(2)将长方形OABC沿数轴水平移动,移动后的长方形记为O′A′B′C′,移动后的长方形O′A′B′C′与原长方形OABC重叠部分(如图2中阴影部分)的面积记为S.
①当S恰好等于原长方形OABC面积的一半时,数轴上点A′表示的数是多少?
②设点A的移动距离AA′=x.
(ⅰ)当S=4时,求x的值;
(ⅱ)D为线段AA′的中点,点E在线段OO′上,且OE=![]() OO′,当点D,E所表示的数互为相反数时,求x的值.
OO′,当点D,E所表示的数互为相反数时,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列变形中:
①由方程![]() =2去分母,得x﹣12=10;
=2去分母,得x﹣12=10;
②由方程![]() x=
x=![]() 两边同除以
两边同除以![]() ,得x=1;
,得x=1;
③由方程6x﹣4=x+4移项,得7x=0;
④由方程2﹣![]() 两边同乘以6,得12﹣x﹣5=3(x+3).
两边同乘以6,得12﹣x﹣5=3(x+3).
错误变形的个数是( )个.
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为配合我市创建省级文明城市,某校对八年级各班文明行为劝导志愿者人数进行了统计,各班统计人数有6名、5名、4名、3名、2名、1名共计六种情况,并制作如下两幅不完整的统计图. 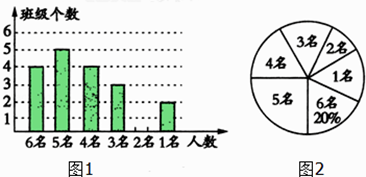
(1)求该年级平均每班有多少文明行为劝导志愿者?并将条形图补充完整;
(2)该校决定本周开展主题实践活动,从八年级只有2名文明行为劝导志愿者的班级中任选两名,请用列表或画树状图的方法,求出所选文明行为劝导志愿者有两名来自同一班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C、G是⊙O上两点,且AC=CG,过点C的直线CD⊥BG于点D,交BA的延长线于点E,连接BC,交OD于点F. 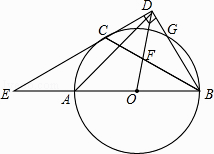
(1)求证:CD是⊙O的切线.
(2)若 ![]() ,求∠E的度数.
,求∠E的度数.
(3)连接AD,在(2)的条件下,若CD= ![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com