练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图,正方形ABCD的面积为12,△ABC是等边三角形,点E在正方形ABCD内,对角线AC上有一点P使PE+PD的和最小,这个最小值为( )

    A. B. C. 3 D.

    【答案】A

    【解析】由于点B与D关于AC对称，所以连接BE，与AC的交点即为P点．此时PD+PE=BE最小，而BE是等边△ABE的边，BE=AB，由正方形ABCD的面积为12，可求出AB的长，从而得出结果．

    解答：解：设BE与AC交于点F（P’），连接BD，

    ∵点B与D关于AC对称，

    ∴P’D=P’B，

    ∴P’D+P’E=P’B+P’E=BE最小．

    即P在AC与BE的交点上时，PD+PE最小，为BE的长度；

    ∵正方形ABCD的面积为12，

    ∴AB=．

    又∵△ABE是等边三角形，

    ∴BE=AB=．

    故所求最小值为．

    故答案为：A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

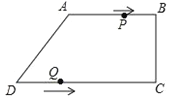
    【题目】如图，在四边形ABCD中，AB∥CD，∠BCD=90°，AB=AD=10cm，BC=8cm，点P从点A出发，以每秒2cm的速度沿线段AB向点B方向运动，点Q从点D出发，以每秒3cm的速度沿线段DC向点C运动，已知动点P、Q同时出发，点P到达B点或点Q到达C点时，P、Q运动停止，设运动时间为t (秒)．

    （1）求CD的长；

    （2）当四边形PBQD为平行四边形时，求t的值；

    （3）在点P、点Q的运动过程中，是否存在某一时刻，使得PQ⊥AB？若存在，请求出t的值并说明理由；若不存在，请说明理

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，一次函数的图像与反比例函数的图像交于第一、三象限内的、两点，与轴交于点，点在轴负半轴上，，且四边形是平行四边形，点的纵坐标为.

    （1）求该反比例函数和一次函数的表达式；

    （2）连接，求的面积；

    （3）直接写出关于的不等式的解集.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】A、B两地相距64 km，甲从A地出发，每小时行14 km，乙从B地出发，每小时行18 km.

    (1)若两人同时出发相向而行，则需经过几小时两人相遇?

    (2)若两人同时出发相向而行，则需经过几小时两人相距16 km?

    (3)若甲在前，乙在后，两人同时同向而行，则几小时后乙超过甲10 km?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，菱形ABCD的对角线AC、BD的长分别是6cm、8cm，AE⊥BC于点E，则AE的长是（ ）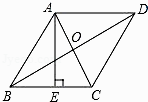
    A. cm
    B. cm
    C. cm
    D.5 cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知∠AOB内部有三条射线，其中OE平分角∠BOC，OF平分∠AOC．

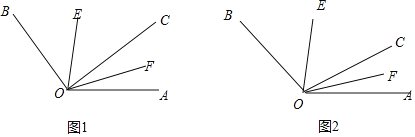
    （1）如图1，若∠AOB=120°，∠AOC=30°，求∠EOF的度数？

    （2）如图2，若∠AOB=α，求∠EOF的度数，（用含α的式子表示）

    （3）若将题中的“平分”的条件改为“∠EOB=∠COB，∠COF=∠COA，且∠AOB=α，求∠EOF的度数．（用含α的式子表示）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算：

    （1） （2）

    （3）

    【答案】(1) ;(2) ;(3) .

    【解析】（1）先化成最简二次根式，再合并同类二次根式即可；

    （2）先算乘法和除法，再合并同类项或同类二次根式即可；

    （3）第一项根据平方差公式计算，第二项根据完全平方公式计算，然后合并同类项或同类二次根式即可；

    (1)原式==

    （2）原式==

    （3）原式==

    点睛：本题考查了二次根式的性质与化简，二次根式的混合运算，熟练掌握二次根式的运算法则是解答本题的关键.

    【题型】解答题
    【结束】
    19

    【题目】（1）化简： （2）解方程：．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，AB是⊙O的直径，C是⊙O上一点，OD⊥BC于点D，过点C作⊙O的切线，交OD的延长线于点E，连接BE．
    （1）求证：BE与⊙O相切；
    （2）连接AD并延长交BE于点F，若OB=9，sin∠ABC= ，求BF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，某渔船在海面上朝正西方向以20海里/时匀速航行，在A处观测到灯塔C在北偏西60°方向上，航行1小时到达B处，此时观察到灯塔C在北偏西30°方向上，若该船继续向西航行至离灯塔距离最近的位置，求此时渔船到灯塔的距离（结果精确到1海里，参考数据： ≈1.732）

    查看答案和解析>>

    同步练习册答案