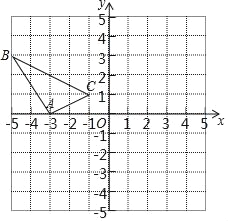
[题目]在边长为1个单位长度的小正方形组成的网格中.建立如图所示的平面直角坐标系△ABC是格点三角形 (1)先作△ABC关于原点O成中心对称的△A1B1C1.再把△A1B1C1向上平移4个单位长度得到△A2B2C2,(2)△A2B2C2与△ABC是否关于某点成中心对称?若是.直接写出对称中心的坐标,若不是.请说明理由．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】在边长为1个单位长度的小正方形组成的网格中，建立如图所示的平面直角坐标系△ABC是格点三角形（顶点在网格线的交点上）

（1）先作△ABC关于原点O成中心对称的△A1B1C1，再把△A1B1C1向上平移4个单位长度得到△A2B2C2；

（2）△A2B2C2与△ABC是否关于某点成中心对称？若是，直接写出对称中心的坐标；若不是，请说明理由．

【答案】（1）作图见解析；（2）△A2B2C2与△ABC关于点（0，2）成中心对称．

【解析】整体分析：

（1）分别作出点A，B，C关于点O的对称点，则得到△A1B1C1，分别作出点A1，B1，C1，向上平移4个单位长度得到△A2B2C2;（2）若两个图形对应点的连线交于一点，则这两个图形关于这点成中心，对称交点是对称中心.

解：(1)如图所示，

(2)是，对称中心的坐标是(0，2).

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

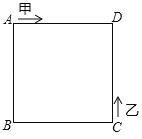
【题目】如图，甲、乙两动点分别从正方形ABCD的顶点A．C同时沿正方形的边开始移动，甲点依顺时针方向环行，乙点依逆时针方向环行．若甲的速度是乙的速度的3倍，则它们第2015次相遇在边________上．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】A、B两地相距64 km，甲从A地出发，每小时行14 km，乙从B地出发，每小时行18 km.

(1)若两人同时出发相向而行，则需经过几小时两人相遇?

(2)若两人同时出发相向而行，则需经过几小时两人相距16 km?

(3)若甲在前，乙在后，两人同时同向而行，则几小时后乙超过甲10 km?

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，已知∠AOB内部有三条射线，其中OE平分角∠BOC，OF平分∠AOC．

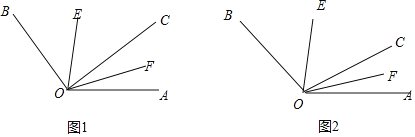
（1）如图1，若∠AOB=120°，∠AOC=30°，求∠EOF的度数？

（2）如图2，若∠AOB=α，求∠EOF的度数，（用含α的式子表示）

（3）若将题中的“平分”的条件改为“∠EOB=∠COB，∠COF=∠COA，且∠AOB=α，求∠EOF的度数．（用含α的式子表示）

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】计算：

（1）（2）

（3）

【答案】(1) ;(2) ;(3) .

【解析】（1）先化成最简二次根式，再合并同类二次根式即可；

（2）先算乘法和除法，再合并同类项或同类二次根式即可；

（3）第一项根据平方差公式计算，第二项根据完全平方公式计算，然后合并同类项或同类二次根式即可；

(1)原式==

（2）原式==

（3）原式==

点睛：本题考查了二次根式的性质与化简，二次根式的混合运算，熟练掌握二次根式的运算法则是解答本题的关键.

【题型】解答题
【结束】
19

【题目】（1）化简：（2）解方程：．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图：在数轴上A点表示数a，B点示数b，C点表示数c，b是最小的正整数，且a，b满足 +(c－7)2=0．

(1) a= ，b= ，c= ．

(2) 若将数轴折叠，使得A点与C点重合，则点B与数表示的点重合．

(3) 点A，B，C开始在数轴上运动，若点A以每秒1个单位长度的速度向左运动，同时，点B和点C分别以每秒2个单位长度和4个单位长度的速度向右运动，假设t秒钟过后，若点A与点B之间的距离表示为AB，点A与点C之间的距离表示为AC，点B与点C之间的距离表示为BC．则AB= ，AC= ，BC= ．(用含t的代数式表示)