
����Ŀ����̽������ͼ�٣���AFH�͡�CHF��ƽ���߽��ڵ�O��EG������O��ƽ����FH���ֱ���AB��CD���ڵ�E��G��
(1)����AFH��60������CHF��50�������EOF��_____�ȣ���FOH��_____�ȣ�
(2)����AFH+��CHF��100�������FOH�Ķ�����
����չ����ͼ�ڣ���AFH�͡�CHI��ƽ���߽��ڵ�O��EG������O��ƽ����FH���ֱ���AB��CD���ڵ�E��G������AFH+��CHF������ֱ��д����FOH�Ķ�����(�ú�a�Ĵ���ʽ��ʾ)

���𰸡���̽������1��30��125����2����FOH��130�㣻����չ����FOH��90�㩁![]() ����
����
��������
��1���ȸ��ݽ�ƽ���ߵĶ��������OFH����FHO �Ķ������ٸ��������ε��ڽǺͶ��������FOH�Ķ�����
��2���ȸ��ݽ�ƽ���ߵĶ��������OFH+��FHO �Ķ������ٸ��������ε��ڽǺͶ��������FOH�Ķ�����
����չ�� �ȸ��ݽ�ƽ���ߵĶ��������OFH��![]() ��AFH����OHI��
��AFH����OHI��![]() ��CHI��
��CHI��![]() ��180��-��CHF�����ٸ�����ֱ��ƽ���ڴ�����ȵ���FOH����OHI����OFH���ɡ�
��180��-��CHF�����ٸ�����ֱ��ƽ���ڴ�����ȵ���FOH����OHI����OFH���ɡ�
��1���ߡ�AFH��60����OFƽ�֡�AFH��
���OFH��30����
�֡�EG��FH��
���EOF����OFH��30������ֱ��ƽ���ڴ����������
�ߡ�CHF��50����OHƽ�֡�CHF��
���FHO��25����
���FOH�У���FOH��180������OFH����OHF��125���������ε��ڽǺͶ�������
�ʴ�Ϊ��30��125��
��2����FOƽ�֡�AFH��HOƽ�֡�CHF��
���OFH��![]() ��AFH����OHF��
��AFH����OHF��![]() ��CHF��
��CHF��
�ߡ�AFH+��CHF��100����
���OFH+��OHF��![]() ����AFH+��CHF����
����AFH+��CHF����![]() ��100����50����
��100����50����
��EG��FH��
���EOF����OFH����GOH����OHF����ֱ��ƽ���ڴ��������.
���EOF+��GOH����OFH+��OHF��50����
�ߡ�EOF+��GOH+��FOH��180���������ε��ڽǺͶ�������
���FOH��180��������EOF+��GOH ����180����50����130����
��չ�ߡ�AFH�͡�CHI��ƽ���߽��ڵ�O��
���OFH��![]() ��AFH����OHI��
��AFH����OHI��![]() ��CHI��
��CHI��
���FOH����OHI����OFH
��![]() ����CHI����AFH��
����CHI����AFH��
��![]() ��180������CHF����AFH��
��180������CHF����AFH��
��![]() ��180��������
��180��������
��90����![]() ����
����
��̽����
��1���ߡ�AFH��60�㣬OFƽ�֡�AFH��
���OFH��30�㣬
�֡�EG��FH��
���EOF����OFH��30�㣻
�ߡ�CHF��50�㣬OHƽ�֡�CHF��
���FHO��25�㣬
���FOH�У���FOH��180�㩁��OFH����OHF��125�㣻
�ʴ�Ϊ��30��125��
��2����FOƽ�֡�AFH��HOƽ�֡�CHF��
���OFH��![]() ��AFH����OHF��
��AFH����OHF��![]() ��CHF��
��CHF��
�ߡ�AFH+��CHF��100�㣬
���OFH+��OHF��![]() ����AFH+��CHF����
����AFH+��CHF����![]() ��100�㣽50�㣮
��100�㣽50�㣮
��EG��FH��
���EOF����OFH����GOH����OHF��
���EOF+��GOH����OFH+��OHF��50�㣮
�ߡ�EOF+��GOH+��FOH��180�㣬
���FOH��180�㩁����EOF+��GOH ����180�㩁50�㣽130�㣮
��չ�ߡ�AFH�͡�CHI��ƽ���߽��ڵ�O��
���OFH��![]() ��AFH����OHI��
��AFH����OHI��![]() ��CHI��
��CHI��
���FOH����OHI����OFH
��![]() ����CHI����AFH��
����CHI����AFH��
��![]() ��180�㩁��CHF����AFH��
��180�㩁��CHF����AFH��
��![]() ��180�㩁����
��180�㩁����
��90�㩁![]() ����
����


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͬһֱ������ϵ�У�����y=mx+m��y=��mx2+2x+2��m�dz�������m��0����ͼ������ǣ� ��
A.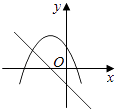
B.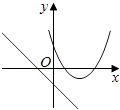
C.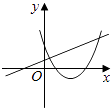
D.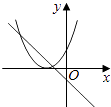
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ����ֱ�Ĺ�·����A��B���أ��������г���A�ص�B�أ�����Ħ�г���B�ص�A�أ�����A�غ�������ԭ·���أ���ͼ�Ǽס���������B�صľ���y��km������ʻʱ��x��h��֮��ĺ���ͼ����ͼ�����������⣺
��1��ֱ��д��y����y����x֮��ĺ�����ϵʽ����д���̣���
��2���������M�����꣬�����õ���������ʾ��ʵ�����壻
������ͼ���жϣ�xȡ��ֵʱ��y����y����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڲ����Ĵ������к�����10ö�Ͱ��������ɣ����dz���ɫ�ⶼ��ͬ�����������������10ö������ɫ��Żأ�������������10�Σ���¼�����µ����ݣ�
���� | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
������ | 1 | 3 | 0 | 2 | 3 | 4 | 2 | 1 | 1 | 3 |
�����������ݣ�������еİ���������Ϊ�� ��
A.60ö
B.50ö
C.40ö
D.30ö
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������һС����Ϊ�˲���С������A��B�ľ��룬������Ա�����һ�ֲ�����������ͼ��ʾ����֪B����CD���е㣬E��BA�ӳ����ϵ�һ�㣬���AE=8.3���DE=30�����DE��EC��cos��D= ![]() ��
�� 
��1����С������A��B�ľ��룻
��2������C��CF��AB��AB���ӳ����ڵ�F����sin��BCF��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
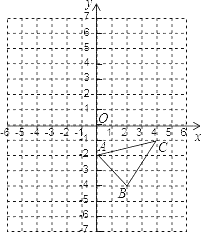
����Ŀ����֪����ͼ����֪��ABC �У����� A��0����2����B��2����4����C��4����1����
��1���������ABC ���� y ��ԳƵ�ͼ�Ρ�A1B1C1��
��2��д����A1B1C1 ���������ꣻ
��3�����ABC �������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����y����m��1��x2��|m|��n��4��
��1����m��nΪ��ֵʱ���˺�����һ�κ�����
��2����m��nΪ��ֵʱ���˺�����������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У�AB=BC����ABC�ա�A1BC1��A1B��AC�ڵ�E��A1C1�ֱ�AC��BC��D��F���㣬�۲첢��������EA1��FC��������������ϵ����֤����Ľ��ۣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com