
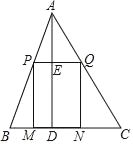
【题目】如图,在△ABC中,点PQ分别在AB,AC上,且PQ∥BC,PM⊥BC于点M,QN⊥BC于点N.AD⊥BC于点D,交PQ于点E,且AD=BC.
(1)求AE:PQ的值;
(2)请探究BM,CN.QN之间的等量关系,并说明理由;
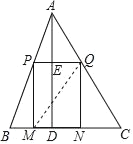
(3)连接MQ,若△ABC的面积等于8,求MQ的最小值.
【答案】(1)AE:PQ=1;(2)QN=BM+CN,理由见解析;(3)当x=4时,MQ有最小值是4![]() .
.
【解析】
(1)根据平行线的性质得到AE⊥PQ,根据相似三角形的性质得到![]() ,求得AE:PQ=AD:BC,由于AD=BC,于是得到结论;
,求得AE:PQ=AD:BC,由于AD=BC,于是得到结论;
(2)根据垂直的定义得到∠PMN=∠MNQ=∠MPQ=90°,推出四边形PMNQ是矩形,得到PQ=MN,PM=ED,等量代换即可得到结论;
(3)根据三角形的面积得到12BCAD=8,求得BC=4,AD=4,设MN=x,则BM+CN=8x,PM=QN=8x,根据勾股定理即可得到结论.
(1)∵PQ∥BC,AD⊥BC,
∴AE⊥PQ,
∵PQ∥BC,
∴△APQ∽△ABC,
![]() ,
,
∴AE:PQ=AD:BC,
∵AD=BC,
∴AE:PQ=AD:BC=1;
(2)QN=BM+CN,
理由是:∵PM⊥BC,QN⊥BC,
∴∠PMN=∠MNQ=∠MPQ=90°,
∴四边形PMNQ是矩形,
∴PQ=MN,PM=ED,
∵AE=PQ,AD=BC,
∴AE+ED=BM+MN+CN,
∴MN+QN=BM+MN+CN,
∴QN=BM+CN;
(3)∵△ABC的面积等于8,
∴![]() BCAD=8,
BCAD=8,
∵AD=BC,
∴![]() BC2=8,
BC2=8,
∴BC=4,AD=4,
设MN=x,则BM+CN=8﹣x,PM=QN=8﹣x,
∵MQ=![]() ,
,
∴当x=4时,MQ有最小值是![]() .
.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:初中数学 来源: 题型:
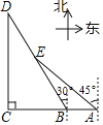
【题目】如图为某景区五个景点A,B,C,D,E的平面示意图,B,A在C的正东方向,D在C的正北方向,D,E在B的北偏西30°方向上,E在A的西北方向上,C,D相距1000![]() m,E在BD的中点处.
m,E在BD的中点处.
(1)求景点B,E之间的距离;
(2)求景点B,A之间的距离.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一组数据a1,a2,a3的平均数为4,方差为3,那么数据a1+2,a2+2,a3+2的平均数和方差分别是( )
A. 4,3B. 6,3C. 3,4D. 6,5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A的坐标为(4,0),点B为y轴上的一动点,将线段AB绕点B顺时针旋转90°得线段BC,若点C恰好落在反比例函数y=![]() 的图象上,则点B的坐标为_____.
的图象上,则点B的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某小区居民使用共享单车次数的情况,某研究小组随机采访该小区的10位居民,得到这10位居民一周内使用共享单车的次数统计如下:
使用次数 | 0 | 5 | 10 | 15 | 20 |
人数 | 1 | 1 | 4 | 3 | 1 |
(1)这10位居民一周内使用共享单车次数的中位数是 次,众数是 次,平均数是 次.
(2)若小明同学把数据“20”看成了“30”,那么中位数,众数和平均数中不受影响的是 .(填“中位数”,“众数”或“平均数”)
(3)若该小区有200名居民,试估计该小区居民一周内使用共享单车的总次数.
查看答案和解析>>
科目:初中数学 来源: 题型:
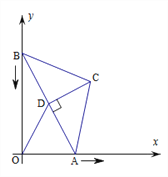
【题目】如图,在△ABC中,BC=AC=5,AB=8,CD为AB边的高,点A在x轴上,点B在y轴上,点C在第一象限,若A从原点出发,沿x轴向右以每秒1个单位长的速度运动,则点B随之沿y轴下滑,并带动△ABC在平面内滑动,设运动时间为t秒,当B到达原点时停止运动
(1)连接OC,线段OC的长随t的变化而变化,当OC最大时,t=____;
(2)当△ABC的边与坐标轴平行时,t=____。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形OABC是矩形,等腰△ODE中,OE=DE,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点B、E在反比例函数y=![]() 的图象上,OA=5,OC=1,则△ODE的面积为( )
的图象上,OA=5,OC=1,则△ODE的面积为( )
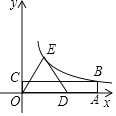
A.2.5B.5C.7.5D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2013年四川南充3分)如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是【 】
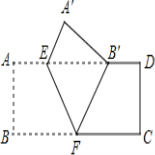
A.12 B. 24 C. 12![]() D. 16
D. 16![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,CD是弦,AB⊥CD,垂足为E,点P在⊙O上,连接BP、PD、BC.若CD=![]() ,sinP=
,sinP=![]() ,则⊙O的直径为( )
,则⊙O的直径为( )

A. 8 B. 6 C. 5 D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com