
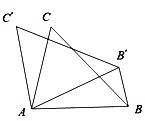
【题目】如图,在△ABC中,∠BAC=75°,以点A为旋转中心,将△ABC绕点A逆时针旋转,得△AB'C',连接BB',若BB'∥AC',则∠BAC′ 的度数是______________.
 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
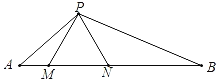
【题目】如图,在△PAB中,M.N是AB上两点,△PMN是等边三角形,∠APM=∠B.
(1)求证:∠A=∠BPN;
(2)求证:MN2=AM·BN;
(3)若AP=![]() ,AM=1,求线段MN,PB的长.
,AM=1,求线段MN,PB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
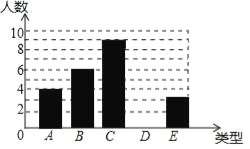
【题目】某校初一年级随机抽取30名学生,对5种活动形式:A、跑步,B、篮球,C、跳绳,D、乒乓球,E、武术,进行了随机抽样调查,每个学生只能选择一种运动行驶,调查统计结果,绘制了不完整的统计图.
(1)将条形图补充完整;
(2)如果初一年级有900名学生,估计喜爱跳绳运动的有多少人?
(3)某次体育课上,老师在5个一样的乒乓球上分别写上A、B、C、D、E,放在不透明的口袋中,每人每次摸出一个球并且只摸一次,然后放回,按照球上的标号参加对应活动,小明和小刚是好朋友,请用树状图或列表法的方法,求他俩恰好是同一种活动形式的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
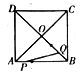
【题目】如图,四边形ABCD是正方形,![]() ,AC、BD交于点O,点P、Q分别是AB、BD上的动点,点P的运动路径是
,AC、BD交于点O,点P、Q分别是AB、BD上的动点,点P的运动路径是![]() ,点Q的运动路径是BD,两点的运动速度相同并且同时结束.若点P的行程为x,
,点Q的运动路径是BD,两点的运动速度相同并且同时结束.若点P的行程为x,![]() 的面积为y,则y关于x的函数图象大致为( )
的面积为y,则y关于x的函数图象大致为( )
A.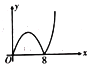 B.
B.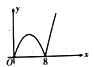 C.
C. D.
D.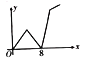
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象分别交x轴、y轴于C,D两点,交反比例函数
的图象分别交x轴、y轴于C,D两点,交反比例函数![]() 图象于A(
图象于A(![]() ,4),B(3,m)两点.
,4),B(3,m)两点.
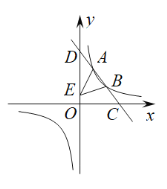
(1)求直线CD的表达式;
(2)点E是线段OD上一点,若![]() ,求E点的坐标;
,求E点的坐标;
(3)请你根据图象直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
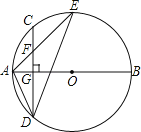
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足![]() ,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.给出下列结论:①△ADF∽△AED;②FG=2;③tan∠E=
,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.给出下列结论:①△ADF∽△AED;②FG=2;③tan∠E=![]() ;④S△DEF=4
;④S△DEF=4![]() .
.
其中正确的是 (写出所有正确结论的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形OABC是一张放在平面直角坐标系中的矩形纸片,点A在x轴上,点C在y轴上,将边BC折叠,使点B落在OA上的点D处,已知折痕CE=5![]() ,且4AE=3AD.
,且4AE=3AD.
①判断△OCD与△ADE是否相似,请说明理由。
②求直线CE与x轴的交点P的坐标。
③是否存在过点D的直线l,使直线l与两坐标轴围成的三角形与直线CE与两坐标轴围成的三角形相似,如果存在,请求出其解析式,如果不存在,请说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
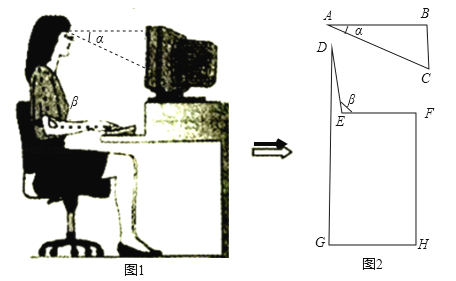
【题目】(2017江西省)如图1,研究发现,科学使用电脑时,望向荧光屏幕画面的“视线角”α约为20°,而当手指接触键盘时,肘部形成的“手肘角”β约为100°.图2是其侧面简化示意图,其中视线AB水平,且与屏幕BC垂直.
(1)若屏幕上下宽BC=20cm,科学使用电脑时,求眼睛与屏幕的最短距离AB的长;
(2)若肩膀到水平地面的距离DG=100cm,上臂DE=30cm,下臂EF水平放置在键盘上,其到地面的距离FH=72cm.请判断此时β是否符合科学要求的100°?
(参考数据:sin69°≈![]() ,cos21°≈
,cos21°≈![]() ,tan20°≈
,tan20°≈![]() ,tan43°≈
,tan43°≈![]() ,所有结果精确到个位)
,所有结果精确到个位)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com