
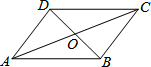
 如图,在?ABCD中,对角线AC与BD交于点O,∠OBC=90°,AC=6,BD=4,则?ABCD的面积是4$\sqrt{5}$.
如图,在?ABCD中,对角线AC与BD交于点O,∠OBC=90°,AC=6,BD=4,则?ABCD的面积是4$\sqrt{5}$. 分析 由平行四边形性质可知S平行四边形ABCD=4•S△BOC,求出△OBC的面积即可.
解答 解:∵四边形ABCD是平行四边形,
∴AO=OC=3,OB=OD=2,
∴S△BOC=S△DOC=S△AOD=S△AOB,
∴S平行四边形ABCD=4•S△BOC,
在RT△BOC中,∵OC=3,OB=2,
∴BC=$\sqrt{O{C}^{2}-O{B}^{2}}$=$\sqrt{{3}^{2}-{2}^{2}}$=$\sqrt{5}$,
∴S平行四边形ABCD=4×$\frac{1}{2}$×2×$\sqrt{5}$=4$\sqrt{5}$.
故答案为4$\sqrt{5}$.
点评 本题考查平行四边形的性质、勾股定理、平行四边形的面积,解题的关键是理解平行四边形的面积与三角形的面积之间的关系,体现了转化的思想,把四边形面积转化为三角形面积,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
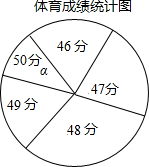 郑州市某中学九年级学生体育中招考试后,为了解本校学生体育测试成绩情况,现从中随机抽取部分学生的体育成绩统计如下,其中如扇形统计图中的圆心角α为36°
郑州市某中学九年级学生体育中招考试后,为了解本校学生体育测试成绩情况,现从中随机抽取部分学生的体育成绩统计如下,其中如扇形统计图中的圆心角α为36°| 体育成绩(分) | 人数(人) | 百分比(%) |
| 46 | 8 | 16 |
| 47 | 24 | |
| 48 | 15 | |
| 49 | m | |
| 50 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com