
【题目】如图,在矩形ABCD中,AB=6cm,BC=4cm.动点E从点B出发,沿着线路BC→CD→DA运动,在BC段的平均速度是1cm/s,在CD段的平均速度是2cm/s,在DA段的平均速度是4cm/s,到点A停止.设△ABE的面积为y(cm2),则y与点E的运动时间t(s)的函数关系图象大致是( )

A. B.
B.
C. D.
D.
【答案】C
【解析】
试题分析:求△ABE的面积y时,可把AB看作底边,E到AB的垂线段看作高.
分三种情况:
①动点E从点B出发,在BC上运动.
∵BC=4cm,动点E在BC段的平均速度是1cm/s,
∴动点E在BC段的运动时间为:4÷1=4(s).
∵y=![]() ABBE=
ABBE=![]() ×6×t=3t,
×6×t=3t,
∴y=3t(0≤t≤4),
∴当0≤t≤4时,y随t的增大而增大,故排除A、B;
②动点E在CD上运动.
∵CD=AB=6cm,动点E在CD段的平均速度是2cm/s,
∴动点E在CD段的运动时间为:6÷2=3(s).
∵y=![]() ABBC=
ABBC=![]() ×6×4=12,
×6×4=12,
∴y=12(4<t≤7),
∴当4<t≤7时,y=12;
③动点E在DA上运动.
∵DA=BC=4cm,动点E在DA段的平均速度是4cm/s,
∴动点E在DA段的运动时间为:4÷4=1(s).
∵y=![]() ABAE=
ABAE=![]() ×6×[4﹣4(t﹣7)]=96﹣12t,
×6×[4﹣4(t﹣7)]=96﹣12t,
∴y=96﹣12t(7<t≤8),
∴当7<t≤8时,y随t的增大而减小,故排除D.
综上可知C选项正确.
故选C.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:
【题目】图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形. 
(1)请用两种不同的方法求图2中阴影部分的面积(直接用含m,n的代数式表示) 方法1:
方法2:
(2)根据(1)中结论,请你写出下列三个代数式之间的等量关系;代数式:(m+n)2 , (m﹣n)2 , mn
(3)根据(2)题中的等量关系,解决如下问题:已知a+b=8,ab=7,求a﹣b和a2﹣b2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列四个命题:
①互为邻补角的两个角的平分线互相垂直;
②经过一点,有且只有一条直线与已知直线平行;
③坐标平面内的点与有序实数对是一一对应的;
④实数a是实数a2的算术平方根.
其中正确命题的序号为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,点C为半径OB上一点,过点C作CD丄AB交半圆O于点D,将△ACD沿AD折叠得到△AED,AE交半圆于点F,连接DF.
(1)求证:DE是半圆的切线:
(2)连接0D,当OC=BC时,判断四边形ODFA的形状,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市招聘教师,对应聘者分别进行教学能力、科研能力、组织能力三项测试,其中甲、乙两人的成绩如下表:(单位:分)

(1)根据实际需要,将教学能力、科研能力、组织能力三项测试得分按5∶3∶2的比确定最后成绩,若按此成绩在甲、乙两人中录用一人,谁将被录用?
(2)按照(1)中的成绩计算方法,将每位应聘者的最后成绩绘制成如图所示的频数分布直方图(每组分数段均包含左端数值,不包含右端数值),并决定由高分到低分录用8人.甲、乙两人能否被录用?请说明理由.
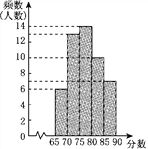
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1+∠2=90°. 
(1)试说明:AB∥CD;
(2)若∠2=25°,求∠3的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com