
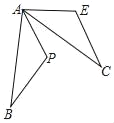
【题目】(1)如图,△AEC绕A点顺时针旋转60°得△APB,∠PAC=20°,求∠BAE.
(2)解不等式组:![]()
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,防洪大堤的横断面是梯形,背水坡AB的坡比i=1:![]() ,且AB=30m,李亮同学在大堤上A点处用高1.5m的测量仪测出高压电线杆CD顶端D的仰角为30°,己知地面BC宽30m,求高压电线杆CD的高度(结果保留三个有效数字,
,且AB=30m,李亮同学在大堤上A点处用高1.5m的测量仪测出高压电线杆CD顶端D的仰角为30°,己知地面BC宽30m,求高压电线杆CD的高度(结果保留三个有效数字,![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一位运动员在距篮下4m处跳起投篮,球运行的路线是抛物线,当球运行的水平距离是2.5m时,达到最大高度3.5m,然后准确落入篮圈.已知篮圈中心到地面的距离为3.05m.
(1)建立如图所示的平面直角坐标系,求抛物线的解析式.
(2)该运动员身高1.8m,在这次跳投中,球在头顶上0.25m处出手,
问:球出手时,他距离地面的高度是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线![]() 的一部分,如图
的一部分,如图

(1)求演员弹跳离地面的最大高度;
(2)已知人梯高BC=3.4米,在一次表演中,人梯到起跳点A的水平距离是4米,问这次表演是否成功?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80m的围网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为xm,矩形区域ABCD的面积为ym2.

(1)求y与x之间的函数关系式,并注明自变量x的取值范围;
(2)x为何值时,y有最大值?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,扇形OAB中,∠AOB=100°,OA=12,C是OB的中点,CD⊥OB交![]() 于点D,以OC为半径的
于点D,以OC为半径的![]() 交OA于点E,则图中阴影部分的面积是( )
交OA于点E,则图中阴影部分的面积是( )

A. 12π+18![]() B. 12π+36
B. 12π+36![]() C. 6π+18
C. 6π+18![]() D. 6π+36
D. 6π+36![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,AB=10cm,BC=6cm,若点P从点A出发,以每秒4cm的速度沿折线A﹣C﹣B﹣A运动,设运动时间为t秒(t>0).

(1)若点P在AC上,且满足△BCP的周长为14cm,求此时t的值;
(2)若点P在∠BAC的平分线上,求此时t的值;
(3)在运动过程中,直接写出当t为何值时,△BCP为等腰三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com