
【题目】如图,△ABC中,∠ACB=90°,AB=10cm,BC=6cm,若点P从点A出发,以每秒4cm的速度沿折线A﹣C﹣B﹣A运动,设运动时间为t秒(t>0).

(1)若点P在AC上,且满足△BCP的周长为14cm,求此时t的值;
(2)若点P在∠BAC的平分线上,求此时t的值;
(3)在运动过程中,直接写出当t为何值时,△BCP为等腰三角形.
【答案】(1)![]()
![]() ;(2)
;(2)![]() ;(3)t为
;(3)t为![]() s或5.3s或5s或
s或5.3s或5s或![]() s时,△BCP为等腰三角形.
s时,△BCP为等腰三角形.
【解析】
(1)根据△BCP的周长为14cm, 可得AP=4t,PC=8-4t,BP=14-PC-BC=4t,根据勾股定理列出方程可求得t的值;
(2)过P作PE⊥AB,设CP=x,根据角平分线的性质和勾股定理列方程式求出CP,由此可求出t;
(3)分类讨论:当CP=CB时,△BCP为等腰三角形,若点P在AC上,根据AP的长即可得到t的值,若点P在AB上,根据P移动的路程易得t的值;当PC=PB时,△BCP为等腰三角形,作PD⊥BC于D,根据等腰三角形的性质得BD=CD,则可判断PD为△ABC的中位线,则AP=0.5AB=5,易得t的值;当BP=BC=6时,△BCP为等腰三角形,易得t的值.
(1)∵△ABC中,∠ACB=90°,AB=10cm,BC=6cm,
∴由勾股定理得![]() ,
,
如图,连接BP,
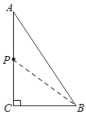
当△BCP的周长为14cm 时,
![]()
在![]() 中根据勾股定理
中根据勾股定理
![]()
即![]()
解得![]() .
.
故此时![]()
![]() ;
;
(2)如图1,过P作PE⊥AB,
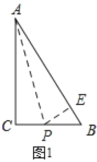
又∵点P恰好在∠BAC的角平分线上,且∠C=90°,AB=10cm,BC=6cm,
∴CP=EP,
∴△ACP≌△AEP(HL),
∴AC=8cm=AE,BE=2,
设CP=x,则BP=6x,PE=x,
∴Rt△BEP中,BE2+PE2=BP2,
即22+x2=(6x)2
解得x=![]() ,
,
∴CP=![]() ,
,
∴CA+CP=8+![]() =
=![]() ,
,
∴![]() ;
;
(3)①如图2,当CP=CB时,△BCP为等腰三角形
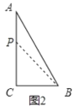
若点P在CA上,则4t=86,
解得t=![]() (s);
(s);
②如图3,
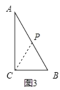
当BP=BC=6时,△BCP为等腰三角形,
∴AC+CB+BP=8+6+6=20,
∴t=20÷4=5(s);
③如图4,
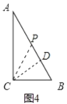
若点P在AB上,CP=CB=6,作CD⊥AB于D,则根据面积法求得CD=4.8,
在Rt△BCD中,由勾股定理得,BD=3.6,
∴PB=2BD=7.2,
∴CA+CB+BP=8+6+7.2=21.2,
此时t=21.2÷4=5.3(s);
④如图5,
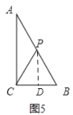
当PC=PB时,△BCP为等腰三角形,作PD⊥BC于D,则D为BC的中点,
∴PD为△ABC的中位线,
∴AP=BP=![]() AB=5,
AB=5,
∴AC+CB+BP=8+6+5=19,
∴t=19÷4=![]() (s);
(s);
综上所述,t为![]() s或5.3s或5s或
s或5.3s或5s或![]() s时,△BCP为等腰三角形.
s时,△BCP为等腰三角形.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.
(1)先从袋子中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,请完成下列表格;
![]()
(2)先从袋子中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个黑球的概率等于![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出一列数![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,…,在这列数中,第50个值等于1的项的序号是( )
,…,在这列数中,第50个值等于1的项的序号是( )
A. 4900 B. 4901 C. 5000 D. 5001
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠B=60°,对角线AC平分角∠BAD,点P是△ABC内一点,连接PA、PB、PC,若PA=6,PB=8,PC=10,则菱形ABCD的面积等于_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦DC交AB于E,过C作⊙O的切线交DB的延长线于M,若AB=4,∠ADC=45°,∠M=75°,则CD的长为( )

A. ![]() B. 2 C.
B. 2 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC中,P为底边BC上任意点,过P作两腰的平行线分别与AB,AC相交于Q,R两点,又P′是P关于直线RQ的对称点,证明:P′在△ABC的外接圆上.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两辆汽车同时从相距330千米的甲、乙两地相向而行,s(千米)表示汽车与甲地的距离,t(分)表示汽车行驶的时间,如图,L1,L2分别表示两辆汽车的s与t的关系.
(1)L1表示哪辆汽车到甲地的距离与行驶时间的关系?
(2)汽车B的速度是多少?
(3)求L1,L2分别表示的两辆汽车的s与t的关系式.
(4)2小时后,两车相距多少千米?
(5)行驶多长时间后,A、B两车相遇?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,等边△ABC中,边长为4,P、Q为AB、AC上的点,将△ABC沿着PQ折叠,使得A点与线段BC上的点D重合,且BD:CD=1:3,则AQ的长度为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com