Question

10．画△ABC，使AB=8，AC=6，AD是BC边上的中线，将△ADC绕点D旋转180°，并画出图形，量一量AD的长，想一想，AD的取值在什么范围内？由此归纳出三角形一边上的中线的取值应满足什么条件，并解答．已知三角形的两边长分别为6和x，第三边上的中线长为4，求x的取值范围．

Answer 1

分析 根据旋转的性质得AD=ED，BE=AC，所以当AB=8，AC=6时，在△ABE中，AE=2AD，BE=AC=6，利用三角形三边的关系得到8-6＜2AD＜8+6，再解不等式组即得到AD的取值范围，由此归纳出三角形一边上的中线的取值应满足的条件；若三角形的两边长分别为6和x，第三边上的中线长为4，利用上述结论有：当x≤6，则6-x＜2•4＜6+x；当x＞6，则x-6＜2•4＜6+x，然后分别解不等式组，最后确定x的取值范围．

解答 解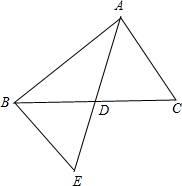：如图，∵AD是BC边上的中线，
∴BD=CD，
∴△ADC绕点D旋转180°得到△EDB，
∴AD=ED，BE=AC，
当AB=8，AC=6时，
在△ABE中，AE=2AD，BE=AC=6，
∴8-6＜2AD＜8+6，
∴AD的取值范围为1＜AD＜7，
由此归纳出三角形一边上的中线的取值应满足的条件为：三角形一边上的中线大于另两边差的一半小于另两边的和的一半；
若三角形的两边长分别为6和x，第三边上的中线长为4，
当x≤6，则6-x＜2•4＜6+x，解得2＜x≤6；
当x＞6，则x-6＜2•4＜6+x，解得6＜x＜14，
所以x的范围为2＜x＜14．

点评 本题考查了作图：旋转变换：根据旋转的性质可知，对应角都相等都等于旋转角，对应线段也相等，由此可以通过作相等的角，在角的边上截取相等的线段的方法，找到对应点，顺次连接得出旋转后的图形．也考查了三角形三边的关系．