
【题目】如图,在ABCD中,对角线AC,BD相交于点O,AB=5,AC=6,BD=8. 
(1)求证:四边形ABCD是菱形;
(2)过点A作AH⊥BC于点H,求AH的长.
【答案】
(1)证明:∵在ABCD中,对角线AC,BD相交于点O,AB=5,AC=6,BD=8,
∴AO= ![]() AC=3,BO=
AC=3,BO= ![]() BD=4,
BD=4,
∵AB=5,且32+42=52,
∴AO2+BO2=AB2,
∴△AOB是直角三角形,且∠AOB=90°,
∴AC⊥BD,
∴四边形ABCD是菱形
(2)解:如图所示:
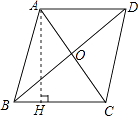
∵四边形ABCD是菱形,
∴BC=AB=5,
∵S△ABC= ![]() ACBO=
ACBO= ![]() BCAH,
BCAH,
∴ ![]() ×6×4=
×6×4= ![]() ×5×AH,
×5×AH,
解得:AH= ![]() .
.
【解析】(1)利用平行四边形的性质结合勾股定理的逆定理得出△AOB是直角三角形,进而得出四边形ABCD是菱形;(2)利用菱形的面积求法得出AH的长.
【考点精析】本题主要考查了平行四边形的性质和菱形的判定方法的相关知识点,需要掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形才能正确解答此题.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案科目:初中数学 来源: 题型:
【题目】已知线段a、b、c满足a:b:c=3:2:6,且a+2b+c=26.
(1)求a、b、c的值;
(2)若线段x是线段a、b的比例中项,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,点D、E分别在BC、AC上,且BD=CE , AD与BE相交于点F . 
(1)试说明△ABD≌△BCE;
(2)△EAF与△EBA相似吗?说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
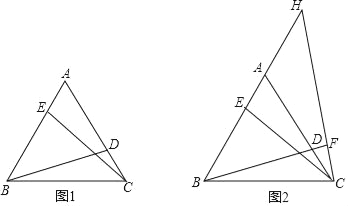
【题目】(1)如图1,点D、E分别是等边△ABC边AC、AB上的点,连接BD、CE,若AE=CD,求证:BD=CE.
(2)如图2,在(1)问的条件下,点H在BA的延长线上,连接CH交BD延长线于点F.若BF=BC,
①求证:EH=EC;
②请你找出线段AH、AD、DF之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx-5的图象经过点A(2,-1).
(1)求k的值;
(2)画出这个函数的图象;
(3)若将此函数的图象向上平移m个单位后与坐标轴围成的三角形的面积为1,请直接写出m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究函数y=x+ ![]() 的图象与性质
的图象与性质
(1)函数y=x+ ![]() 的自变量x的取值范围是;
的自变量x的取值范围是;
(2)下列四个函数图象中,函数y=x+ ![]() 的图象大致是
的图象大致是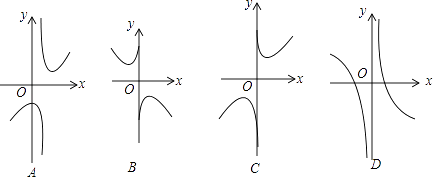
(3)对于函数y=x+ ![]() ,求当x>0时,y的取值范围.
,求当x>0时,y的取值范围.
请将下面求解此问题的过程补充完整:
解:∵x>0
∴y=x+ ![]()
=( ![]() )2+(
)2+( ![]() )2
)2
=( ![]() ﹣
﹣ ![]() )2+
)2+
∵( ![]() ﹣
﹣ ![]() )2≥0,
)2≥0,
∴y .
(4)若函数y= ![]() ,则y的取值范围是
,则y的取值范围是
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,反比例函数y1= ![]() 的图象与一次函数y2=ax+b的图象交于点A(1,3)和B(﹣3,m).
的图象与一次函数y2=ax+b的图象交于点A(1,3)和B(﹣3,m).
(1)求反比例函数y1= ![]() 和一次函数y2=ax+b的表达式;
和一次函数y2=ax+b的表达式;
(2)点C 是坐标平面内一点,BC∥x 轴,AD⊥BC 交直线BC 于点D,连接AC.若AC= ![]() CD,求点C的坐标.
CD,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点H在⊙O上,E是 ![]() 的中点,过点E作EC⊥AH,交AH的延长线于点C.连接AE,过点E作EF⊥AB于点F.
的中点,过点E作EC⊥AH,交AH的延长线于点C.连接AE,过点E作EF⊥AB于点F.
(1)求证:CE是⊙O的切线;
(2)若FB=2,tan∠CAE= ![]() ,求OF的长.
,求OF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里装有三个分别写有数字6,﹣2,7的小球,它们的形状、大小、质地完全相同,先从盒子里随机抽取一个小球,记下数字后放回盒子,摇匀后再随机取出一个小球,记下数字,请你用画树状图或列表的方法求两次取出小球上的数字和大于10的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com