
【题目】甲乙两人在相同条件下完成了10次射击训练,两人的成绩如图所示。

根据以上信息,整理分析数据如下:
平均成绩/环 | 中位数/环 | 方差/环 | |
甲 | ______ | 7 | 1.2 |
乙 | 7 | ______ | ______ |
(1)完成表格;
(2)根据训练成绩,你认为选派哪一名队员参赛更好?为什么?
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,E、F分别是BC边,CD边的中点,AE、AF分别交BD于点G,H,设△AGH的面积为S1,平行四边形ABCD的面积为S2,则S1:S2的值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,直径BD交AC于E,过O作FG⊥AB,交AC于F,交AB于H,交⊙O于G.
(1)求证:OFDE=OE2OH;
(2)若⊙O的半径为12,且OE:OF:OD=2:3:6,求阴影部分的面积.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习了统计知识后,数学老师请数学兴趣小组的同学就本班同学的上学方式进行了一次调查统计.如图甲乙是数学兴趣小组的同学们通过手机和整理数据后,绘制的两幅不完整的统计图.
请你根据图中提供的信息,解答一下的问题:
(1)在扇形统计图中,计算出“步行”部分所应对的圆心角的度数.
(2)请问该班共有多少名学生?
(3)在图中将表示“乘车”的部分补充完整.
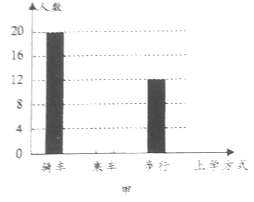
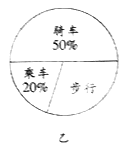
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BF和CE分别是钝角△ABC(∠ABC是钝角)中AC、AB边上的中线,又BF⊥CE,垂足是G,过点G作GH⊥BC,垂足为H.
(1)求证:GH2=BHCH;
(2)若BC=20,并且点G到BC的距离是6,则AB的长为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“新中梁山隧道”于2017年11月21日开放通行,原中梁山隧道将封闭升级,扩容改造工程预计2018年3月全部完工,届时将实现双向8车道通行,隧道通行能力将增加一倍,沿线交通拥堵状况将有所缓解.图中线段AB表示该工程的部分隧道.无人勘测机从隧道侧的A点出发时,测得C点正上方的E点的仰角为45°,无人机飞行到E点后,沿着坡度i=1:3的路线EB飞行,飞行到D点正上方的F点时,测得A点的俯角为12°,其中EC=100米,A、B、C、D、E、F在同一平面内,则隧道AD段的长度约为( )米,(参考数据:tan12°≈0.2,cosl2°≈0.98)

A. 200 B. 250 C. 300 D. 540
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算或化简:
(1)sin45°cos60°﹣cos45°sin30°;
(2)5tan30°﹣2(cos60°﹣sin60°);
(3)(![]() tan30°)2005(2
tan30°)2005(2![]() sin45°)2004;
sin45°)2004;
(4)![]() (2cos45°﹣tan45°)﹣(tan60°+sin30°)0﹣(2sin45°﹣1)﹣1.
(2cos45°﹣tan45°)﹣(tan60°+sin30°)0﹣(2sin45°﹣1)﹣1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的对角线AC、BD相交于点O,AE平分∠BAD,分别交BC、BD于点E、P,连接OE,∠ADC=60°,AB=![]() BC=1,则下列结论:
BC=1,则下列结论:
①∠CAD=30°②BD=![]() ③S平行四边形ABCD=ABAC④OE=
③S平行四边形ABCD=ABAC④OE=![]() AD⑤S△APO=
AD⑤S△APO=![]() ,正确的个数是( )
,正确的个数是( )

A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】折叠圆心为![]() 、半径为
、半径为![]() 的圆形纸片,使圆周上的某一点
的圆形纸片,使圆周上的某一点![]() 与圆心
与圆心![]() 重合.对圆周上的每一点,都这样折叠纸片,从而都有一条折痕.那么,所有折痕所在直线上点的全体为( )
重合.对圆周上的每一点,都这样折叠纸片,从而都有一条折痕.那么,所有折痕所在直线上点的全体为( )
A. 以![]() 为圆心、半径为
为圆心、半径为![]() 的圆周 B. 以
的圆周 B. 以![]() 为圆心、半径为
为圆心、半径为![]() 的圆周
的圆周
C. 以![]() 为圆心、半径为
为圆心、半径为![]() 的圆内部分 D. 以
的圆内部分 D. 以![]() 为圆心、半径为
为圆心、半径为![]() 的圆周及圆外部分
的圆周及圆外部分
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com