
【题目】如图,△ABC内接于⊙O,直径BD交AC于E,过O作FG⊥AB,交AC于F,交AB于H,交⊙O于G.
(1)求证:OFDE=OE2OH;
(2)若⊙O的半径为12,且OE:OF:OD=2:3:6,求阴影部分的面积.(结果保留根号)

【答案】(1)证明:∵BD是直径,∴∠DAB=90°。
∵FG⊥AB,∴DA∥FO。∴△FOE∽△ADE。
∴![]() ,即OFDE=OEAD。
,即OFDE=OEAD。
∵O是BD的中点,DA∥OH,∴AD=2OH。∴OFDE=OE2OH。
(2)解:∵⊙O的半径为12,且OE:OF:OD=2:3:6,∴OE=4,ED=8,OF=6。
代入(1)中![]() ,得AD=12。∴OH=
,得AD=12。∴OH=![]() AD=6。
AD=6。
在Rt△ABC中,OB=2OH,∴∠OBH=30°,∴∠BOH=60°。
∴BH=BOsin60°=12×![]() 。
。
∴S阴影=S扇形GOB﹣S△OHB=![]() 。
。
【解析】(1)由BD是直径,根据圆周角定理,可得∠DAB=90°,又由FG⊥AB,可得FG∥AD,即可判定△FOE∽△ADE,根据相似三角形的对应边成比例,即可得![]() ,然后由O是BD的中点,DA∥OH,可得AD=2OH,则可证得OFDE=OE2OH。
,然后由O是BD的中点,DA∥OH,可得AD=2OH,则可证得OFDE=OE2OH。
(2)由⊙O的半径为12,且OE:OF:OD=2:3:6,即可求得OE,DE,OF的长,由![]() ,求得AD的长,又由在Rt△ABC中,OB=2OH,可求得∠BOH=60°,继而可求得BH的长,又由S阴影=S扇形GOB﹣S△OHB,即可求得答案。
,求得AD的长,又由在Rt△ABC中,OB=2OH,可求得∠BOH=60°,继而可求得BH的长,又由S阴影=S扇形GOB﹣S△OHB,即可求得答案。


科目:初中数学 来源: 题型:
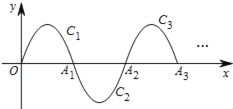
【题目】如图,我们把抛物线y=﹣x(x﹣3)(0≤x≤3)记为C1,它与x轴交于点O,A1将C1绕点A1旋转180°得C2,交x 轴于另一点A2;将C2绕点A2旋转180°得C3,交x 轴于另一点A3;…;如此进行下去,直至得C2016.①C1的对称轴方程是_____;②若点P(6047,m)在抛物线C2016上,则m=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
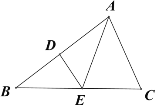
【题目】如图,在△ABC中,AB的垂直平分线分别交AB,BC于点D,E,∠B=30°,∠BAC=80°,且BC+AC=12cm,①求∠CAE的度数;②求△AEC的周长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假期间,某学校计划用彩色的地面砖铺设教学楼门前一块矩形操场ABCD的地面.已知这个矩形操场地面的长为100m,宽为80m,图案设计如图所示:操场的四角为小正方形,阴影部分为四个矩形,四个矩形的宽都为小正方形的边长,在实际铺设的过程总,阴影部分铺红色地面砖,其余部分铺灰色地面砖.
(1)如果操场上铺灰色地面砖的面积是铺红色地面砖面积的4倍,那么操场四角的每个小正方形边长是多少米?
(2)如果灰色地面砖的价格为每平方米30元,红色地面砖的价格为每平方米20元,学校现有15万元资金,问这些资金是否能购买所需的全部地面砖?如果能购买所学的全部地面砖,则剩余资金是多少元?如果不能购买所需的全部地面砖,教育局还应该至少给学校解决多少资金?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(﹣4,a),B(﹣1,2)是一次函数y1=kx+b与反比例函数y2=![]() (m<0)图象的两个交点,AC⊥x轴于C.
(m<0)图象的两个交点,AC⊥x轴于C.

(1)求出k,b及m的值.
(2)根据图象直接回答:在第二象限内,当y1>y2时,x的取值范围是 ________.
(3)若P是线段AB上的一点,连接PC,若△PCA的面积等于![]() ,求点P坐标.
,求点P坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=-x2+(m-1)x+m与y轴交于点(0,3).
(1)求抛物线的解析式;
(2)求抛物线与x轴的交点坐标;
(3)画出这条抛物线大致图象;
(4)根据图象回答:
① 当x取什么值时,y>0 ?
② 当x取什么值时,y的值随x的增大而减小?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,L1,L2分别表示一种白炽灯和一种节能灯的费用y(费用=灯的售价+电费,单位:元)与照明时间x(h)的函数图像,假设两种灯的使用寿命都是2000h,照明效果一样.
(1)根据图像分别求出L1,L2的函数关系式.
(2)当照明时间为多少时,两种灯的费用相等?
(3)小亮房间计划照明2500h,他买了一个白炽灯和一个节能灯,请你帮他设计最省钱的用灯方法(直接给出答案,不必写出解答过程).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两人在相同条件下完成了10次射击训练,两人的成绩如图所示。

根据以上信息,整理分析数据如下:
平均成绩/环 | 中位数/环 | 方差/环 | |
甲 | ______ | 7 | 1.2 |
乙 | 7 | ______ | ______ |
(1)完成表格;
(2)根据训练成绩,你认为选派哪一名队员参赛更好?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△EBD中,∠ABC=∠DBE=90°,AB=CB,BE=BD,连接AE,CD,AE与CD交于点M,AE与BC交于点N.
(1)求证:AE=CD;
(2)求证:AE⊥CD;
(3)连接BM,有以下两个结论:①BM平分∠CBE;②MB平分∠AMD.其中正确的有 (请写序号,少选、错选均不得分).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com