
【题目】暑假期间,某学校计划用彩色的地面砖铺设教学楼门前一块矩形操场ABCD的地面.已知这个矩形操场地面的长为100m,宽为80m,图案设计如图所示:操场的四角为小正方形,阴影部分为四个矩形,四个矩形的宽都为小正方形的边长,在实际铺设的过程总,阴影部分铺红色地面砖,其余部分铺灰色地面砖.
(1)如果操场上铺灰色地面砖的面积是铺红色地面砖面积的4倍,那么操场四角的每个小正方形边长是多少米?
(2)如果灰色地面砖的价格为每平方米30元,红色地面砖的价格为每平方米20元,学校现有15万元资金,问这些资金是否能购买所需的全部地面砖?如果能购买所学的全部地面砖,则剩余资金是多少元?如果不能购买所需的全部地面砖,教育局还应该至少给学校解决多少资金?

【答案】(1)操场四角的每个小正方形边长是5米;
(2)这些资金不能购买所需的全部地面砖,教育局还应该至少给学校解决19.95﹣15=4.95万元资金.
【解析】
试题分析:(1)设小正方形的边长为x米,表示出里边大矩形的长为(100﹣2x)米,宽为(80﹣2x)米,利用灰色部分的面积=4个小正方形的面积+里边大矩形的面积,红色部分面积=上下两个矩形面积+左右两个矩形面积,根据灰色地面砖的面积是铺红色地面砖面积的4倍列出关于x的方程,求出方程的解得到x的值,即为小正方形的边长;
(2)设铺矩形广场地面的总费用为y元,广场四角的小正方形的边长为x米,根据等量关系“总费用=铺白色地面砖的费用+铺绿色地面砖的费用”列出y关于x的函数,求得最小值,与15万元比较可得是否够用.
试题解析:(1)设操场四角的每个小正方形边长是x米,根据题意,
得:4x2+(100﹣2x)(80﹣2x)=4[2x(100﹣2x)+2x(80﹣2x)],
整理,得:x2﹣45x+200=0,
解得:x1=5,x2=40(舍去),
故操场四角的每个小正方形边长是5米;
(2)设铺矩形广场地面的总费用为y元,广场四角的小正方形的边长为x米,
则,y=30×[4x2+(100﹣2x)(80﹣2x)]+20×[2x(100﹣2x)+2x(80﹣2x)]
即:y=80x2﹣3600x+240000
配方得,y=80(x﹣22.5)2+199500
当x=22.5时,y的值最小,最小值为19.95万元>15万元,
故这些资金不能购买所需的全部地面砖,教育局还应该至少给学校解决19.95﹣15=4.95万元资金.


 每课必练系列答案
每课必练系列答案科目:初中数学 来源: 题型:
【题目】如图是重叠的两个直角三角形,将三角形ABC沿AB方向平移2cm后,得到三角形DEF,若CH=2cm,EF=4cm,则图中阴影部分面积为cm2 . 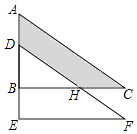
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校准备修建一个面积为20m2的矩形花圃,它的长比宽多10m.设花圃的宽为xm,则可列方程为( )
A.x(x﹣10)=20
B.2x+2(x﹣10)=20
C.x(x+10)=20
D.2x+2(x+10)=20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一例.如图,这个三角形的构造法则:两腰上的数都是1,其余每个数均为其上方左右两数之和,它给出了(a+b)n(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应(a+b)2=a2+2ab+b2展开式中的系数;第四行的四个数1,3,3,1,恰好对应着(a+b)3=a3+3a2b+3ab2+b2展开式中的系数等等. 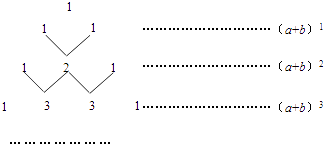
(1)根据上面的规律,则(a+b)5的展开式= .
(2)利用上面的规律计算:25﹣5×24+10×23﹣10×22+5×2﹣1= .
查看答案和解析>>
科目:初中数学 来源: 题型:
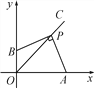
【题目】如图,已知点P(2m-1,6m-5)在第一象限的角平分线OC 上,AP⊥BP,点A在x轴上,点 B在y 轴上.
(1)求点P 的坐标;
(2)当∠APB绕点P旋转时,OA+OB的值是否发生变化?若变化,求出其变化范围;若不变,求出这个定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列从左到右的变形是因式分解的是( )
A. (﹣a+b)2=a2﹣2ab+b2 B. m2﹣4m+3=(m﹣2)2﹣1
C. ﹣a2+9b2=﹣(a+3b)(a﹣3b) D. (x﹣y)2=(x+y)2﹣4xy
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一个长为2a,宽为2b的长方形(a>b),沿图中虚线用剪刀均匀分成四块相同小长方形,然后按图2方式拼成一个大正方形 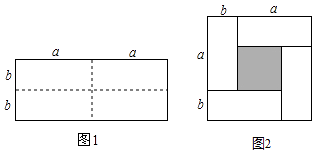
(1)你认为图2中大正方形的边长为;小正方形(阴影部分)的边长为 . (用含a、b代数式表示)
(2)仔细观察图2,利用图2中存在的面积关系,直接写出下列三个代数式:(a﹣b)2 , (a+b)2 , 4ab之间的等量关系
(3)利用(2)中得出的结论解决下面的问题:已知a+b=7,ab=6,求代数式(a﹣b)的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com