
【题目】如图是重叠的两个直角三角形,将三角形ABC沿AB方向平移2cm后,得到三角形DEF,若CH=2cm,EF=4cm,则图中阴影部分面积为cm2 . 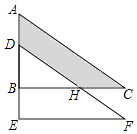
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】某商场购进一批服装,每件进价为200元,由于换季滞销,商场决定将这种服装按标价的六折销售,若打折后每件服装仍能获利20%,则该服装标价是( )
A.350元
B.400元
C.450元
D.500元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填入相应集合的括号内:
-(-2),-![]() ,200%,0,3.14,,
,200%,0,3.14,, ![]() ,
, ![]() ,-
,- ![]() ,2.13133133313…
,2.13133133313…
正分数集合:{ …};
负有理数集合:{ …};
整数集合:{ …};
无理数集合:{ …};
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点E、F分别在直线AB,CD上,点P在AB、CD之间,连结EP、FP,如图1,过FP上的点G作GH∥EP,交CD于点H,且∠1=∠2.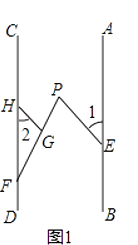
(1)求证:AB∥CD;
(2)如图2,将射线FC沿FP折叠,交PE于点J,若JK平分∠EJF,且JK∥AB,则∠BEP与∠EPF之间有何数量关系,并证明你的结论;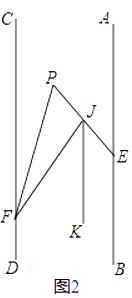
(3)如图3,将射线FC沿FP折叠,将射线EA沿EP折叠,折叠后的两射线交于点M,当EM⊥FM时,求∠EPF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在△ABC中,∠ACB为锐角,点D为射线BC上一点,连接AD,以AD为一边且在AD的右侧作正方形ADEF,连接CF.
(1)如果AB=AC,∠BAC=90°,
①当点D在线段BC上时(与点B不重合),如图(2),线段CF,BD所在直线的位置关系为______,线段CF,BD的数量关系为________;
②当点D在线段BC的延长线上时,如图(3),①中的结论是否仍然成立,并说明理由;
(2)如果AB≠AC,∠BAC是锐角,点D在线段BC上,当∠ACB满足什么条件时,CF⊥BC(点C、F不重合),并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市生产运营用水和居民家庭用水的总和为5.8亿立方米,其中居民家庭用水比生产运营用水的3倍还多0.6亿立方米,问生产运营用水和居民家庭用水各多少亿立方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假期间,某学校计划用彩色的地面砖铺设教学楼门前一块矩形操场ABCD的地面.已知这个矩形操场地面的长为100m,宽为80m,图案设计如图所示:操场的四角为小正方形,阴影部分为四个矩形,四个矩形的宽都为小正方形的边长,在实际铺设的过程总,阴影部分铺红色地面砖,其余部分铺灰色地面砖.
(1)如果操场上铺灰色地面砖的面积是铺红色地面砖面积的4倍,那么操场四角的每个小正方形边长是多少米?
(2)如果灰色地面砖的价格为每平方米30元,红色地面砖的价格为每平方米20元,学校现有15万元资金,问这些资金是否能购买所需的全部地面砖?如果能购买所学的全部地面砖,则剩余资金是多少元?如果不能购买所需的全部地面砖,教育局还应该至少给学校解决多少资金?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com