
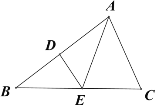
【题目】如图,在△ABC中,AB的垂直平分线分别交AB,BC于点D,E,∠B=30°,∠BAC=80°,且BC+AC=12cm,①求∠CAE的度数;②求△AEC的周长。
科目:初中数学 来源: 题型:
【题目】如图,在一次夏令营活动中,小明从营地A出发,沿北偏东60°方向走了![]() m 到达点B,然后再沿北偏西30°方向走了50m到达目的地C。
m 到达点B,然后再沿北偏西30°方向走了50m到达目的地C。

(1)求A、C两点之间的距离;
(2)确定目的地C在营地A的北偏东多少度方向。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】形如:![]() 的函数叫二次函数,它的图象是一条抛物线.类比一元一次方程的解可以看成两条直线的交点的横坐标;则一元二次方程
的函数叫二次函数,它的图象是一条抛物线.类比一元一次方程的解可以看成两条直线的交点的横坐标;则一元二次方程![]() 的解可以看成抛物线
的解可以看成抛物线![]() 与直线
与直线![]() (
(![]() 轴)的交点的横坐标;也可以看成是抛物线
轴)的交点的横坐标;也可以看成是抛物线![]() 与直线
与直线![]() ________的交点的横坐标;也可以看成是抛物线
________的交点的横坐标;也可以看成是抛物线![]() ________与直线
________与直线![]() 的交点的横坐标;
的交点的横坐标;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,E、F分别是BC边,CD边的中点,AE、AF分别交BD于点G,H,设△AGH的面积为S1,平行四边形ABCD的面积为S2,则S1:S2的值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
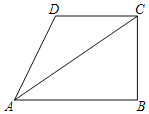
【题目】如图,在四边形ABCD中,AB∥CD,∠B=90°,连接AC,∠DAC=∠BAC.
(1)求证:AD=DC;
(2)若∠D=120°,求∠ACB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2﹣(m+1)x+m
(1)求证:抛物线与x轴一定有交点;
(2)若抛物线与x轴交于A(x1,0),B(x2,0)两点,x1<0<x2,且![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我国南宋数学家杨辉(约13世纪)所著的《详解九章算术》(1261年)一书中,用下图的三角形解释二项和的乘方规律.杨辉在注释中提到,在他之前北宋数学家贾宪(1050年左右)也用过上述方法,因此我们称这个三角形为“杨辉三角”或“贾宪三角”.杨辉三角两腰上的数都是![]() ,其余每一个数为它上方(左右)两数的和.事实上,这个三角形给出了
,其余每一个数为它上方(左右)两数的和.事实上,这个三角形给出了![]()
![]() 的展开式(按
的展开式(按![]() 的次数由大到小的顺序)的系数规律.例如,此三角形中第三行的
的次数由大到小的顺序)的系数规律.例如,此三角形中第三行的![]() 个数
个数![]() ,恰好对应着
,恰好对应着![]() 展开式中的各项系数,第四行的
展开式中的各项系数,第四行的![]() 个数
个数![]() ,恰好对应着
,恰好对应着![]() 展开式中的各项系数,等等.请依据上面介绍的数学知识,解决下列问题:
展开式中的各项系数,等等.请依据上面介绍的数学知识,解决下列问题:
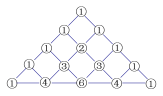
(1)写出![]() 的展开式;
的展开式;
(2)利用整式的乘法验证你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,直径BD交AC于E,过O作FG⊥AB,交AC于F,交AB于H,交⊙O于G.
(1)求证:OFDE=OE2OH;
(2)若⊙O的半径为12,且OE:OF:OD=2:3:6,求阴影部分的面积.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算或化简:
(1)sin45°cos60°﹣cos45°sin30°;
(2)5tan30°﹣2(cos60°﹣sin60°);
(3)(![]() tan30°)2005(2
tan30°)2005(2![]() sin45°)2004;
sin45°)2004;
(4)![]() (2cos45°﹣tan45°)﹣(tan60°+sin30°)0﹣(2sin45°﹣1)﹣1.
(2cos45°﹣tan45°)﹣(tan60°+sin30°)0﹣(2sin45°﹣1)﹣1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com