
【题目】形如:![]() 的函数叫二次函数,它的图象是一条抛物线.类比一元一次方程的解可以看成两条直线的交点的横坐标;则一元二次方程
的函数叫二次函数,它的图象是一条抛物线.类比一元一次方程的解可以看成两条直线的交点的横坐标;则一元二次方程![]() 的解可以看成抛物线
的解可以看成抛物线![]() 与直线
与直线![]() (
(![]() 轴)的交点的横坐标;也可以看成是抛物线
轴)的交点的横坐标;也可以看成是抛物线![]() 与直线
与直线![]() ________的交点的横坐标;也可以看成是抛物线
________的交点的横坐标;也可以看成是抛物线![]() ________与直线
________与直线![]() 的交点的横坐标;
的交点的横坐标;
科目:初中数学 来源: 题型:
【题目】如图,已知AD、AE分别是△ABC的中线、高,且AB=4cm,AC=3cm,请解答下列问题:
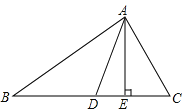
(1)△ABD与△ACD的面积大小有怎样的关系?并说明理由.
(2)△ABD与△ACD的周长之差是多少?
(3)当AE=2.5cm ,BC=6cm时,试求△ABD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新泰特产专卖店销售樱桃,其进价为每千克30元,按每千克50元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低1元,则平均每天的销售量可增加10千克,若该专卖店销售这种樱桃想要平均每天获利2240元,请回答:
(1)每千克樱桃应降价多少元?
(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,我们把抛物线y=﹣x(x﹣3)(0≤x≤3)记为C1,它与x轴交于点O,A1将C1绕点A1旋转180°得C2,交x 轴于另一点A2;将C2绕点A2旋转180°得C3,交x 轴于另一点A3;…;如此进行下去,直至得C2016.①C1的对称轴方程是_____;②若点P(6047,m)在抛物线C2016上,则m=_____.
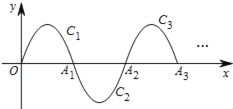
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数的图象经过(-2,-1),(1,1)两点,则下列关于此二次函数的说法正确的是【 】
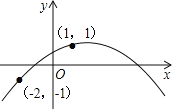
A.y的最大值小于0 B.当x=0时,y的值大于1
C.当x=-1时,y的值大于1 D.当x=-3时,y的值小于0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形![]() 的边长为4,点
的边长为4,点![]() 是△
是△![]() 的中心,
的中心,![]() .绕点
.绕点![]() 旋转
旋转![]() ,分别交线段
,分别交线段![]() 于
于![]() 两点,连接
两点,连接![]() ,给出下列四个结论:①
,给出下列四个结论:①![]() ;②
;②![]() ;③四边形
;③四边形![]() 的面积始终等于
的面积始终等于![]() ;④△
;④△![]() 周长的最小值为6,上述结论中正确的个数是( )
周长的最小值为6,上述结论中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
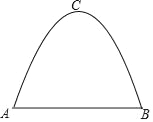
【题目】一条单车道的抛物线形隧道如图所示.隧道中公路的宽度AB=8m,隧道的最高点C到公路的距离为6m.
(1)建立适当的平面直角坐标系,求抛物线的表达式;
(2)现有一辆货车的高度是4.4m,货车的宽度是2m,为了保证安全,车顶距离隧道顶部至少0.5m,通过计算说明这辆货车能否安全通过这条隧道.
查看答案和解析>>
科目:初中数学 来源: 题型:
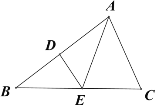
【题目】如图,在△ABC中,AB的垂直平分线分别交AB,BC于点D,E,∠B=30°,∠BAC=80°,且BC+AC=12cm,①求∠CAE的度数;②求△AEC的周长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,L1,L2分别表示一种白炽灯和一种节能灯的费用y(费用=灯的售价+电费,单位:元)与照明时间x(h)的函数图像,假设两种灯的使用寿命都是2000h,照明效果一样.
(1)根据图像分别求出L1,L2的函数关系式.
(2)当照明时间为多少时,两种灯的费用相等?
(3)小亮房间计划照明2500h,他买了一个白炽灯和一个节能灯,请你帮他设计最省钱的用灯方法(直接给出答案,不必写出解答过程).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com