
【题目】新泰特产专卖店销售樱桃,其进价为每千克30元,按每千克50元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低1元,则平均每天的销售量可增加10千克,若该专卖店销售这种樱桃想要平均每天获利2240元,请回答:
(1)每千克樱桃应降价多少元?
(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?
科目:初中数学 来源: 题型:
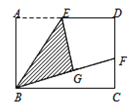
【题目】如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠 得到△GBE,且点G在矩形ABCD内部.将BG延长交DC 于点F,若DC=nDF,则 ![]() =______.
=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一次夏令营活动中,小明从营地A出发,沿北偏东60°方向走了![]() m 到达点B,然后再沿北偏西30°方向走了50m到达目的地C。
m 到达点B,然后再沿北偏西30°方向走了50m到达目的地C。

(1)求A、C两点之间的距离;
(2)确定目的地C在营地A的北偏东多少度方向。
查看答案和解析>>
科目:初中数学 来源: 题型:
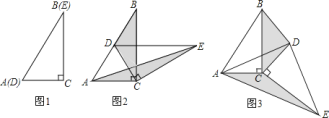
【题目】如图![]() ,将两个完全相同的三角形纸片
,将两个完全相同的三角形纸片![]() 和
和![]() 重合放置,其中
重合放置,其中![]() ,
,![]() ,若固定
,若固定![]() ,将
,将![]() 绕点
绕点![]() 旋转.
旋转.
![]() 当
当![]() 绕点
绕点![]() 旋转到点
旋转到点![]() 恰好落在
恰好落在![]() 边上时,如图
边上时,如图![]() ,则此时旋转角为________(用含的式子表示).
,则此时旋转角为________(用含的式子表示).
![]() 当
当![]() 绕点
绕点![]() 旋转到如图
旋转到如图![]() 所示的位置时,小杨同学猜想:
所示的位置时,小杨同学猜想:![]() 的面积与
的面积与![]() 的面积相等,试判断小杨同学的猜想是否正确,若正确,请你证明小杨同学的猜想.若不正确,请说明理由.
的面积相等,试判断小杨同学的猜想是否正确,若正确,请你证明小杨同学的猜想.若不正确,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 三个顶点的坐标分别为
三个顶点的坐标分别为![]() ,
,![]() ,
,![]() 。
。
(1)请画出![]() 关于
关于![]() 轴对称后得到的
轴对称后得到的![]() ;
;
(2)直接写出点![]() ,点
,点![]() ,点
,点![]() 的坐标;
的坐标;
(3)在![]() 轴上寻找一个点
轴上寻找一个点![]() ,使
,使![]() 的周长最小,并直接写出
的周长最小,并直接写出![]() 的周长的最小值。
的周长的最小值。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC、△CDE都是等腰三角形,且CA=CB,CD=CE,∠ACB=∠DCE=α,AD,BE相交于点O,点M,N分别是线段AD,BE的中点,以下4个结论:①AD=BE;②∠DOB=180°-α;③△CMN是等边三角形;④连OC,则OC平分∠AOE.正确的是( )
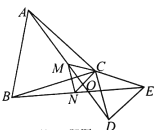
A.①②③B.①②④C.①③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】形如:![]() 的函数叫二次函数,它的图象是一条抛物线.类比一元一次方程的解可以看成两条直线的交点的横坐标;则一元二次方程
的函数叫二次函数,它的图象是一条抛物线.类比一元一次方程的解可以看成两条直线的交点的横坐标;则一元二次方程![]() 的解可以看成抛物线
的解可以看成抛物线![]() 与直线
与直线![]() (
(![]() 轴)的交点的横坐标;也可以看成是抛物线
轴)的交点的横坐标;也可以看成是抛物线![]() 与直线
与直线![]() ________的交点的横坐标;也可以看成是抛物线
________的交点的横坐标;也可以看成是抛物线![]() ________与直线
________与直线![]() 的交点的横坐标;
的交点的横坐标;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我国南宋数学家杨辉(约13世纪)所著的《详解九章算术》(1261年)一书中,用下图的三角形解释二项和的乘方规律.杨辉在注释中提到,在他之前北宋数学家贾宪(1050年左右)也用过上述方法,因此我们称这个三角形为“杨辉三角”或“贾宪三角”.杨辉三角两腰上的数都是![]() ,其余每一个数为它上方(左右)两数的和.事实上,这个三角形给出了
,其余每一个数为它上方(左右)两数的和.事实上,这个三角形给出了![]()
![]() 的展开式(按
的展开式(按![]() 的次数由大到小的顺序)的系数规律.例如,此三角形中第三行的
的次数由大到小的顺序)的系数规律.例如,此三角形中第三行的![]() 个数
个数![]() ,恰好对应着
,恰好对应着![]() 展开式中的各项系数,第四行的
展开式中的各项系数,第四行的![]() 个数
个数![]() ,恰好对应着
,恰好对应着![]() 展开式中的各项系数,等等.请依据上面介绍的数学知识,解决下列问题:
展开式中的各项系数,等等.请依据上面介绍的数学知识,解决下列问题:
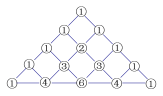
(1)写出![]() 的展开式;
的展开式;
(2)利用整式的乘法验证你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com